If two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
To prove that the bisectors of any pair of alternate interior angles formed by two parallel lines intersected by a transversal are parallel, we can follow these steps:
1. Draw the Figure:
- Let lines AB and CD be two parallel lines, and let XY be the transversal that intersects them.
- Mark the points of intersection as follows: let point E be the intersection of line XY with line AB and point F be the intersection of line XY with line CD.
2. Identify Alternate Interior Angles:
- The alternate interior angles formed are ∠AEF and ∠EFD. By the property of parallel lines cut by a transversal, we know that these angles are equal:
∠AEF=∠EFD
3. Draw the Angle Bisectors:
- Let GE be the bisector of angle AEF and FH be the bisector of angle EFD. By definition of angle bisector, we have:
∠AEG=∠GEFand∠EFH=∠EFDH
- Thus, we can express the angles as:
∠AEG=12∠AEFand∠EFH=12∠EFD
4. Establish the Equality of the Bisected Angles:
- Since ∠AEF = ∠EFD, we can write:
12∠AEF=12∠EFD
- Therefore, we have:
∠GEF=∠EFH
5. Conclude that the Bisectors are Parallel:
- Since ∠GEF and ∠EFH are alternate interior angles and they are equal, by the property of parallel lines, we conclude that:
GE∥FH
Conclusion:
Thus, we have proved that the bisectors of any pair of alternate interior angles formed by two parallel lines intersected by a transversal are parallel.
- Let lines AB and CD be two parallel lines, and let XY be the transversal that intersects them.
- Mark the points of intersection as follows: let point E be the intersection of line XY with line AB and point F be the intersection of line XY with line CD.
- The alternate interior angles formed are ∠AEF and ∠EFD. By the property of parallel lines cut by a transversal, we know that these angles are equal:
∠AEF=∠EFD
- Let GE be the bisector of angle AEF and FH be the bisector of angle EFD. By definition of angle bisector, we have:
∠AEG=∠GEFand∠EFH=∠EFDH
- Thus, we can express the angles as:
∠AEG=12∠AEFand∠EFH=12∠EFD
- Since ∠AEF = ∠EFD, we can write:
12∠AEF=12∠EFD
- Therefore, we have:
∠GEF=∠EFH
- Since ∠GEF and ∠EFH are alternate interior angles and they are equal, by the property of parallel lines, we conclude that:
GE∥FH
Thus, we have proved that the bisectors of any pair of alternate interior angles formed by two parallel lines intersected by a transversal are parallel.
Topper's Solved these Questions
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Example
13 Videos
- LINES AND ANGLESBOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A
12 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)
24 Videos
- MEAN , MEDIAN AND MODE OF UNGROUPED DATA BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)
18 Videos
Similar Questions
Knowledge Check
If two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
AequalBadjacentCSupplementaryDComplementaryTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
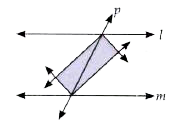 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquareIf two parallel lines are cut by a transversal, then the alternate interior angles are equal
ATRUEBFALSECCannot be determinedDNone of these
If two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal; the bisector of any two corresponding angles are parallel.
View SolutionTwo parallel lines are cut by a transversal , then which of the following are true ?
1. Pair of alternate interior angles are equal.
2. Pair of corresponding angles are equal
3. Pair of interior angles on the same side of the transversal are supplementary.
View Solution
