If x and y are connected parametrically by the equation , without eliminating parameter , find dydx
x=asec(θ),y=btan(θ)Solution in Punjabi
The correct Answer is:B
Step by step video & image solution for If x and y are connected parametrically by the equation , without eliminating parameter , find dy/dx x = a sec(theta) , y = b tan(theta) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERCISE 5: MATCHING TYPE QUESTIONS
4 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Single Integer Answer Type Questions)
16 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Statement I And Ii Type Questions)
15 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statement of Colume I with values of Column II.
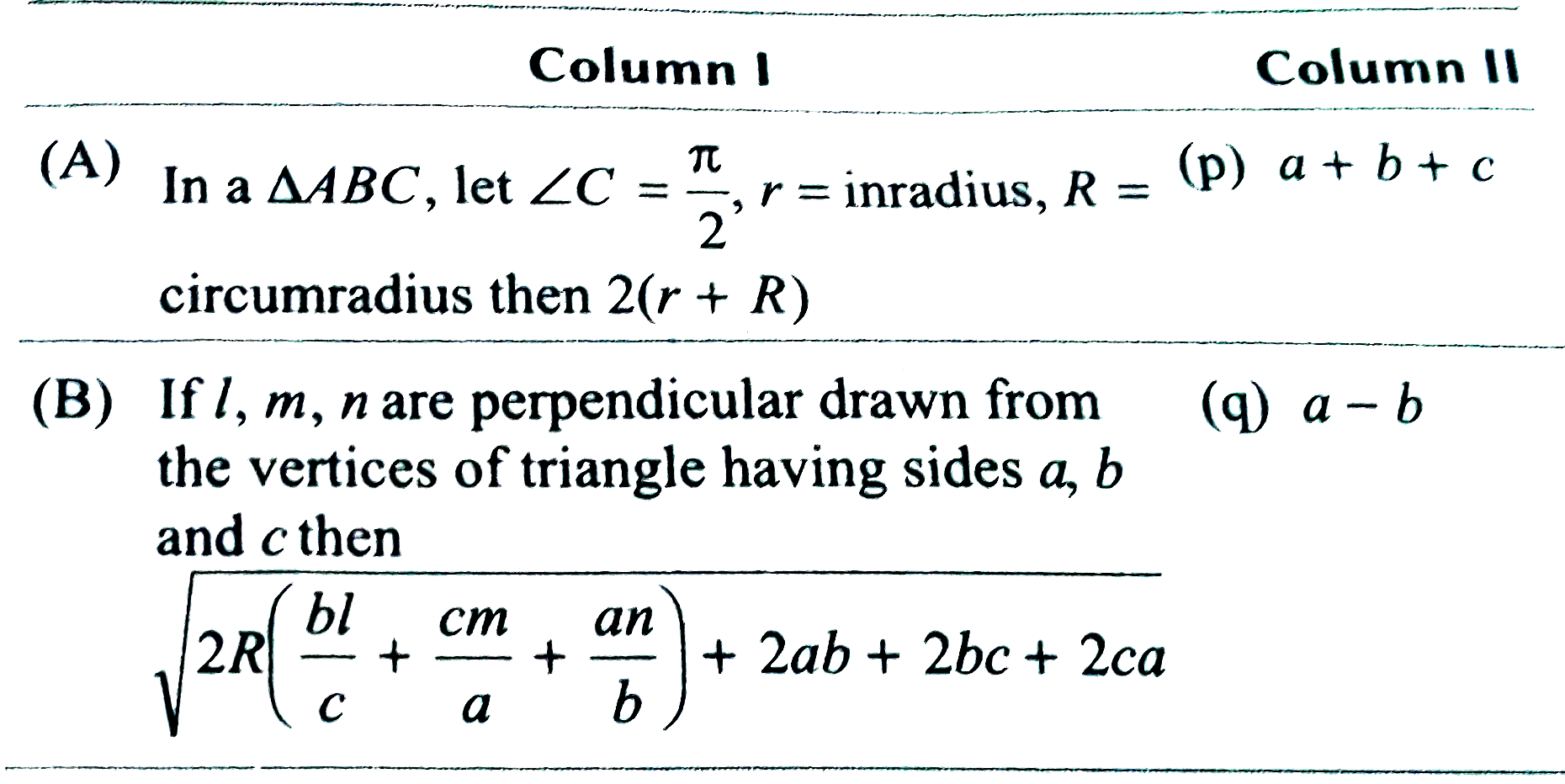
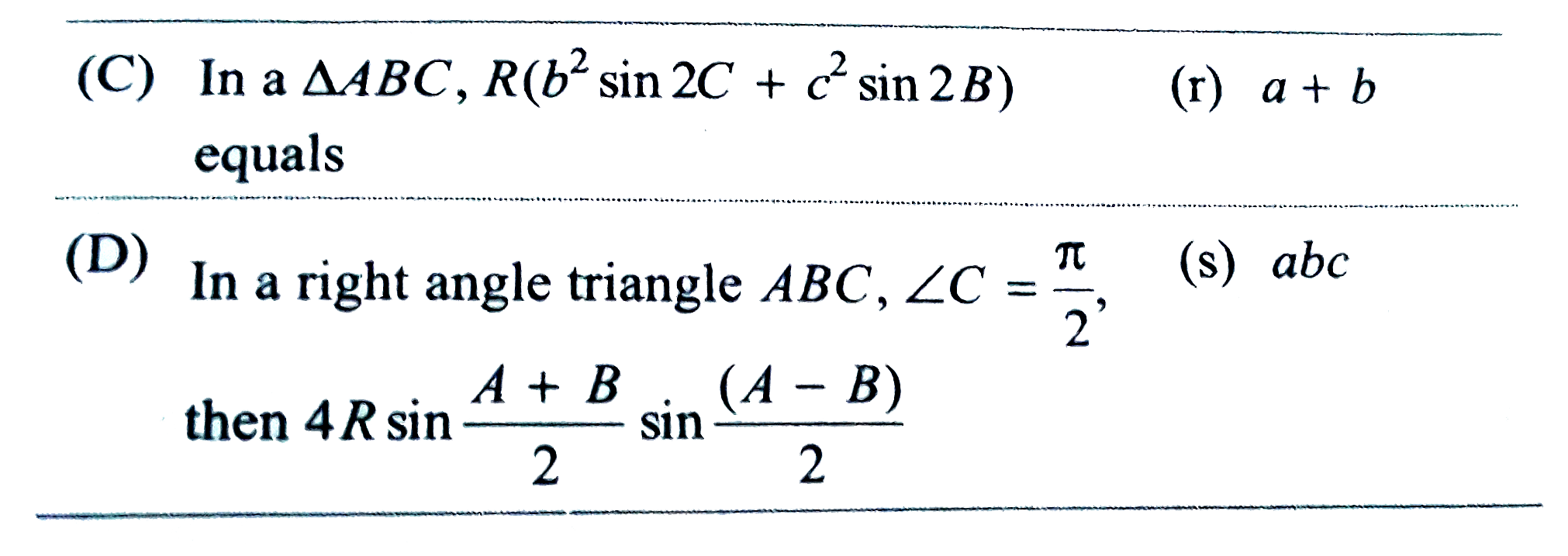
View SolutionIf in ΔABC,∠C=π8,a=√2andb=√2+√2 then find the measure of angle A (in degree).
View SolutionIn a triangle ABC,a3+b3+c3=c2(a+b+c) (All symbol used have usual meaning in a triangle.) Statement-1: The value of ∠C=60∘. Statement-2: ΔABC must be equilateral.
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=asecθ,y=btanθ
View SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=a(θ−sinθ),y=a(1+cosθ)
View SolutionIf x and y are connected parametrically by the equations given, without eliminating the parameter, Find dydx.
x=acosθ,y=bcosθ
View SolutionFind dydx, if x and y are connected parametrically by the equations, given below without eliminating the parameter:
x=a(θ−sinθ),y=b(1+cosθ)
View SolutionIf x and y are connected parametrically by the equations given in, without eliminating the parameter, find dydx.
x=a(cosθ+logtanθ2),y=asinθ.
View SolutionIf x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dydx.
x=asecθ,y=btanθ.
View SolutionIf x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dydx.
x=asecθ,y=btanθ.
View Solutionx=asecθ,y=btanθ.
View SolutionIf x and y are connected parametrically by the equations, without eliminating the parameter, Find dydx.
x=a(θ−sinθ),y=a(1+cosθ).
View SolutionIf x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dydx.
x=asecθ,y=btanθ.
View SolutionIf x and y are connected parametrically by the equations given in Exercises 1 to 10, without eliminating the parameter, Find dydx.
x=asecθ,y=btanθ.
View Solution
