If x coordinates of two points B and C are the roots of equation x2+4x+3=0 and their y coordinates are the roots of equation x2−x−6=0. If x coordinate of B is less than x coordinate of C and y coordinate of B is greater than the y coordinate of C and coordinates of a third point A be (3, -5), find the length of the bisector of the interior angle at A.
Step by step video & image solution for If x coordinates of two points B and C are the roots of equation x^(2)+4x +3=0 and their y coordinates are the roots of equation x^(2)-x-6=0. If x coordinate of B is less than x coordinate of C and y coordinate of B is greater than the y coordinate of C and coordinates of a third point A be (3, -5), find the length of the bisector of the interior angle at A. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
x coordinates of two points B and C are the roots of equation x2+4x+3=0 and their y coordinates are the roots of equation x2−x−6=0. If x coordinate of B is less than the x coordinate of C and y coordinate of B is greater than the y coordinate of C and coordinates of a third point A be (3,−5), find the length of the bisector of the interior angle at A.
View SolutionIf a point lies on X-axis, then what are its y and z co-ordinates ?
View Solution
Knowledge Check
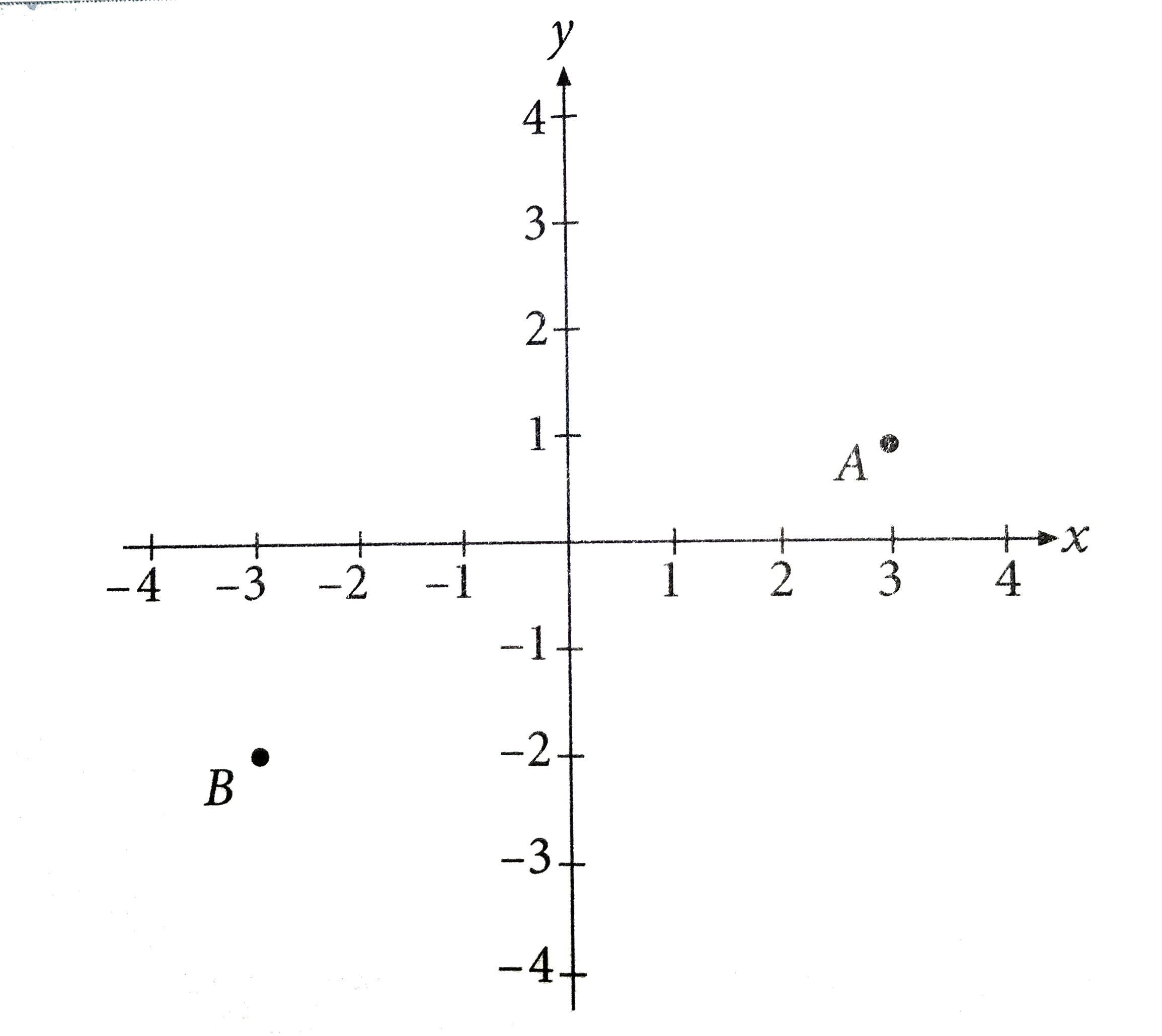
In the xy-plane above, what is the value of the x-coordinates of Point A minus the y-coordinates of Point B?A−2B−1C3D5P is a point on the line segment joining the points (3,2,−1)and(6,2,−2). If the x-coordinate of P is 5, then its y-coordinate is
A1B−1C2D−2
The abscissae of two points AandB are the roots of the equaiton x2+2x−a2=0 and the ordinats are the roots of the equaiton y2+4y−b2=0. Find the equation of the circle with AB as its diameter. Also find the coordinates of the centre and the length of the radius of the circle.
View SolutionWrite the coordinates the reflections of point (3, 5) in X and Y -axes.
View SolutionThe x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2,−5)andR(−3,6), then find the coordinates of P.
View SolutionFind the coordinates of the centre, foci and equation of directrix of the hyperbola x2−3y2−4x=8.
View SolutionFind the eccentricity, coordinates of the foci, equations of directrices and length of the latus rectum of the hyperbola 3x2−y2=4
View SolutionFind the equation of a curve passing through the point (0,1) if the slope of the tangent to the curve at any point (x,y) is equal to the sum of the x coordinate (abscissa) and the product of the x coordinate and y coordinate (ordinate) of that point.
View Solution
