x coordinates of two points B and C are the roots of equation x2+4x+3=0 and their y coordinates are the roots of equation x2−x−6=0. If x coordinate of B is less than the x coordinate of C and y coordinate of B is greater than the y coordinate of C and coordinates of a third point A be (3,−5), find the length of the bisector of the interior angle at A.
The correct Answer is:14√23 units
To solve the problem step by step, we will follow these steps:
Step 1: Find the x-coordinates of points B and C
We need to solve the quadratic equation x2+4x+3=0.
Using the factorization method:
x2+4x+3=(x+1)(x+3)=0
Thus, the roots are:
x=−1andx=−3
Since the x-coordinate of B is less than that of C, we assign:
B(−3,yB)andC(−1,yC)
Step 2: Find the y-coordinates of points B and C
Now, we solve the quadratic equation x2−x−6=0.
Using the factorization method:
x2−x−6=(x−3)(x+2)=0
Thus, the roots are:
y=3andy=−2
Since the y-coordinate of B is greater than that of C, we assign:
B(−3,3)andC(−1,−2)
Step 3: Find the length of AB
Given point A is A(3,−5), we will use the distance formula to find the length of AB:
AB=√(xB−xA)2+(yB−yA)2
Substituting the coordinates:
AB=√(−3−3)2+(3−(−5))2
=√(−6)2+(8)2=√36+64=√100=10
Step 4: Find the length of AC
Now we find the length of AC:
AC=√(xC−xA)2+(yC−yA)2
Substituting the coordinates:
AC=√(−1−3)2+(−2−(−5))2
=√(−4)2+(3)2=√16+9=√25=5
Step 5: Use the Angle Bisector Theorem
According to the Angle Bisector Theorem:
BDDC=ABAC=105=2
This means that BD:DC=2:1.
Step 6: Find the coordinates of point D using the section formula
Using the section formula, where D divides BC in the ratio 2:1:
D(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)
Here, m1=2, m2=1, B(−3,3), and C(−1,−2):
D(2⋅(−1)+1⋅(−3)2+1,2⋅(−2)+1⋅32+1)
Calculating the coordinates:
D(−2−33,−4+33)=D(−53,−13)
Step 7: Find the length of AD
Now we find the length of AD:
AD=√(xD−xA)2+(yD−yA)2
Substituting the coordinates:
AD=√(3−−53)2+(−5−−13)2
Calculating:
=√(3+53)2+(−5+13)2
=√(93+53)2+(−153+13)2
=√(143)2+(−143)2
=√1969+1969=√3929=14√23
Final Answer
The length of the bisector of the interior angle at A is 14√23.
---
x2+4x+3=(x+1)(x+3)=0
Thus, the roots are:
x=−1andx=−3
Since the x-coordinate of B is less than that of C, we assign:
B(−3,yB)andC(−1,yC)
x2−x−6=(x−3)(x+2)=0
Thus, the roots are:
y=3andy=−2
Since the y-coordinate of B is greater than that of C, we assign:
B(−3,3)andC(−1,−2)
AB=√(xB−xA)2+(yB−yA)2
Substituting the coordinates:
AB=√(−3−3)2+(3−(−5))2
=√(−6)2+(8)2=√36+64=√100=10
AC=√(xC−xA)2+(yC−yA)2
Substituting the coordinates:
AC=√(−1−3)2+(−2−(−5))2
=√(−4)2+(3)2=√16+9=√25=5
BDDC=ABAC=105=2
This means that BD:DC=2:1.
D(m1x2+m2x1m1+m2,m1y2+m2y1m1+m2)
Here, m1=2, m2=1, B(−3,3), and C(−1,−2):
D(2⋅(−1)+1⋅(−3)2+1,2⋅(−2)+1⋅32+1)
Calculating the coordinates:
D(−2−33,−4+33)=D(−53,−13)
AD=√(xD−xA)2+(yD−yA)2
Substituting the coordinates:
AD=√(3−−53)2+(−5−−13)2
Calculating:
=√(3+53)2+(−5+13)2
=√(93+53)2+(−153+13)2
=√(143)2+(−143)2
=√1969+1969=√3929=14√23
The length of the bisector of the interior angle at A is 14√23.
Topper's Solved these Questions
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 1
10 Videos
- COORDINATE SYSTEM AND COORDINATES BOOK - ARIHANT MATHS ENGLISHCHAPTER - COORDINATE SYSTEM AND COORDINATES EXERCISE - Exercise For Session 2
19 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
20 Videos
- DEFINITE INTEGRALBOOK - ARIHANT MATHS ENGLISHCHAPTER - DEFINITE INTEGRALEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
If a point lies on X-axis, then what are its y and z co-ordinates ?
View SolutionThe abscissae of two points AandB are the roots of the equaiton x2+2x−a2=0 and the ordinats are the roots of the equaiton y2+4y−b2=0. Find the equation of the circle with AB as its diameter. Also find the coordinates of the centre and the length of the radius of the circle.
View Solution
Knowledge Check
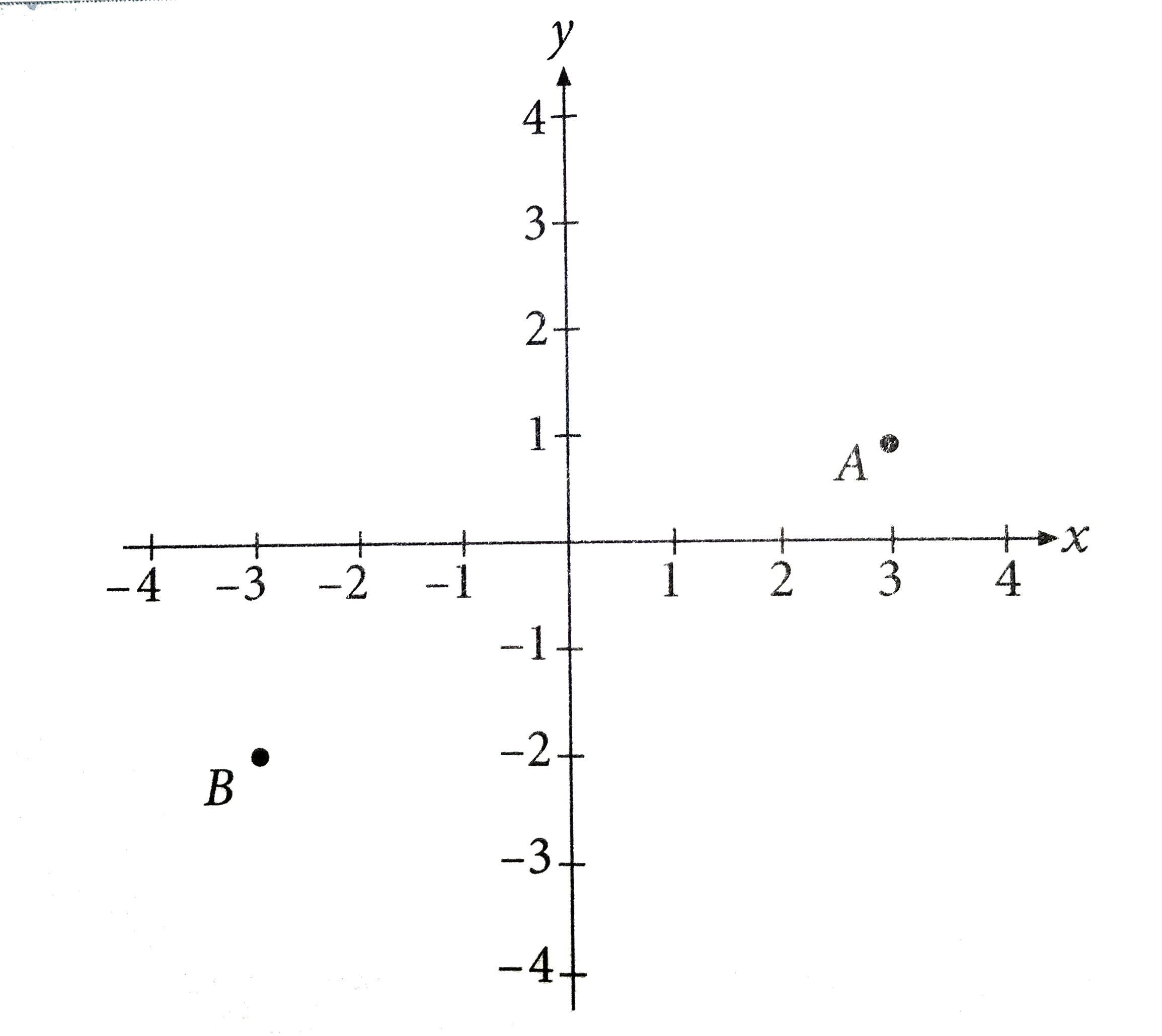
In the xy-plane above, what is the value of the x-coordinates of Point A minus the y-coordinates of Point B?A−2B−1C3D5P is a point on the line segment joining the points (3,2,−1)and(6,2,−2). If the x-coordinate of P is 5, then its y-coordinate is
A1B−1C2D−2
Write the coordinates the reflections of point (3, 5) in X and Y -axes.
View SolutionFind the coordinates of the centre, foci and equation of directrix of the hyperbola x2−3y2−4x=8.
View SolutionIf the linex+y=1touches the parabola y2−y+x=0, then the coordinates of the point of contact are:
View SolutionLet A,B,C be the feet of perpendicular drawn from a point P to x,y and z-axes respectively. Find the coordinates of A,B,C if coordinates of P are : (3,−5,1)
View SolutionThe x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q(2,−5)andR(−3,6), then find the coordinates of P.
View SolutionFind the coordinates of the points on the curve y=x2+3x+4, the tangents at which pass through the origin.
View Solution
