If x∈[1,2] , then find the range of f(x)=tanx
Video Solution
Text Solution
The correct Answer is:(−∞,tan2]∪[tan1,∞)
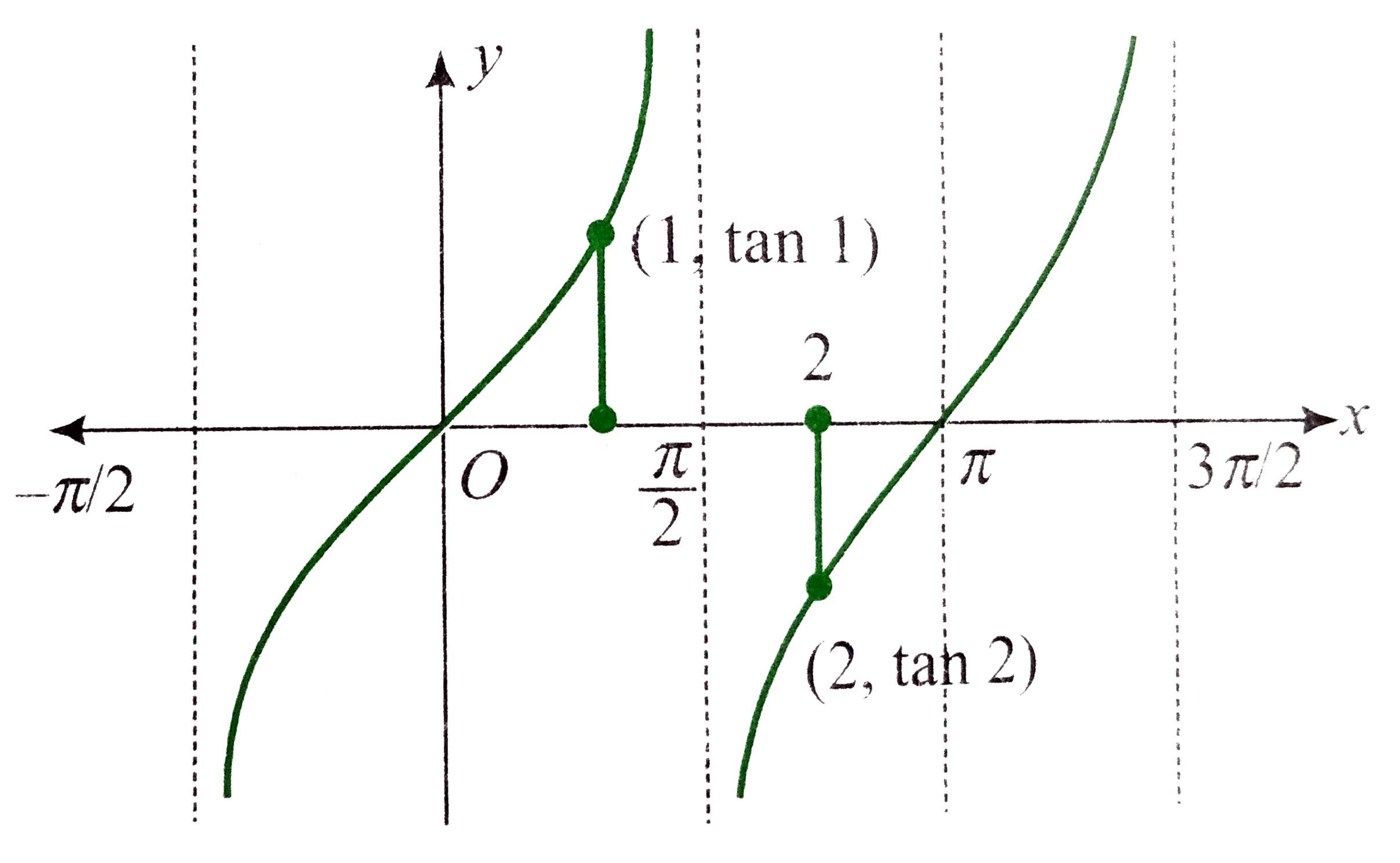
f(x)=tanx,x∈[1,2]
Here, the limited values of x are given.
The best way to get the range of tanx for such values of x is graphical one.
Consider the graph of f(x)=tanx for x∈[1,2].
Clearly, from the graph, tan∈(−∞,tan2]∪[tan1,∞).
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.7
5 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.8
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.5
5 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
If x∈[1,2] , then find the range of f(x)=tanx
View SolutionFind the range of f(x)=x2+2
View Solutionfind the range of f(x)=|x+2|−3
View SolutionFind the range of f(x)=2x2−1
View SolutionFind the range of ,f(x)=14−x2
View SolutionFind the range of f(x)=sgn(x2−2x+3).
View SolutionFind the range of
f(x)=x2−2|x|+3
View SolutionFind the range of
f(x)=∣∣x2−3x+2∣∣
View SolutionFind the range of f(x)=x1+x2
View SolutionFind the range of f(x)=sin2x−sinx+1.
View Solution
