If X is a random variable such that σ(X)=2.6, then σ(1−4X) is equal to, Solution in Bengali
7.8
−10.4
13
10.4
Step by step video & image solution for If X is a random variable such that sigma(X) = 2.6, then sigma(1-4X) is equal to, by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
If (2≤r≤n). then nCr+2.nCr+2 is equal to
View SolutionIf I=limx→0sin⎛⎜⎝ex−x−1−x22x2⎞⎟⎠, then limit
View SolutionIf the standard deviation of a variable X is σ , then standard deviation of variable aX+bc is
View SolutionIf m and σ2 are the mean and variance of the random variable X whose distribution is given by
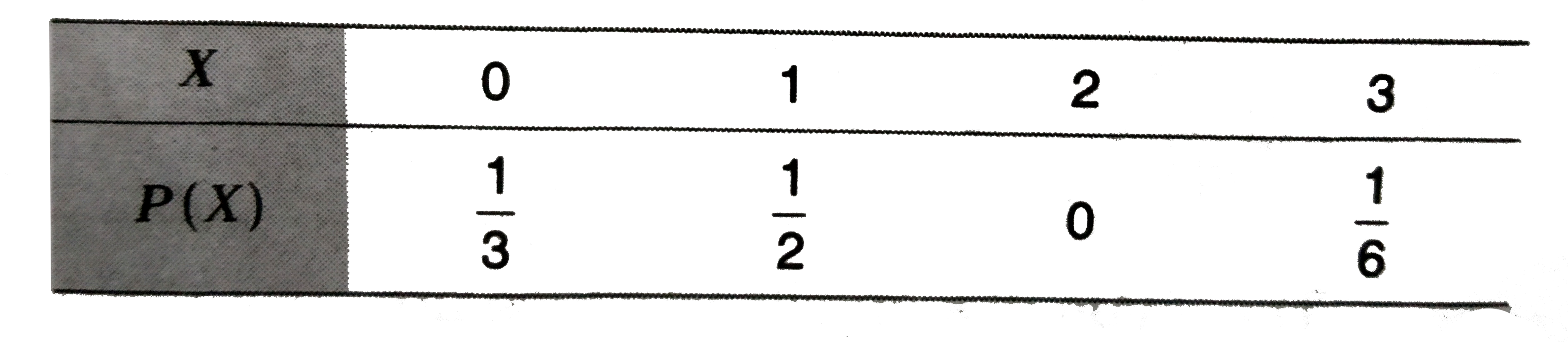
View SolutionIf X is a random variable such that σ(X)=2.6, then σ(1−4X) is equal to,
View Solutionकिसी बंटन के लिए निम्नलिखित सूचनाएँ हैं : n=10,Σx=60,Σx2=1000, तो मानक विचलन बराबर है :
View SolutionIf μ and σ2 are the mean and variance of the discrete random variable X, and E(X+3)=10 and E(X+3)2=116, find μ and σ2.
View SolutionIf mandσ2 are the mean and variance of the random variable X, whose distribution is given by:
X=x:0123P(X=x):1312016
View SolutionIf the variance of the random variable X is 9 the S.D .of the random variable -4X+8 is
View SolutionIf X is a bernoulli 's random variable with parameter p then the variance σ2 is
View SolutionIf X is a random variable such that σ(X)=2.6, then σ(1−4X) is equal to
View Solutionএকটি যদৃচ্ছ চল X এর ক্ষেত্রে σ(X)=2.6 হলে σ(1−4X) -এর মান হবে –
View SolutionIf m and σ2 are the mean and variance of random variable x, whose distribution is given by then sum of m and σ2 is
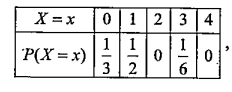
View SolutionIf the standard deviation of a variable x is σ , then standard deviation of variable aX+bc is (a).σ (b) acσ (c) ∣∣ac∣∣σ (d) aσ+bc
View SolutionIf the variance of the observations x _(1), x _(2) ,... X _(n) is sigma ^(2) then the variance of alpha x _(1) , sigma x _(2),... , x sigma x _(n) , alpha ne 0, is
View SolutionLet X be a random variable with distribution.
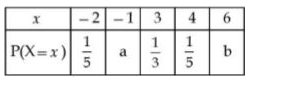
If the mean of X is 2.3 and variance of X is σ2, then 100σ2 is equal to :
View Solution
