If X is a random variable such that σ(X)=2.6, then σ(1−4X) is equal to
7.8
−10.4
13
10.4
The correct Answer is:D
To find the value of σ(1−4X) given that σ(X)=2.6, we will follow these steps:
Step 1: Understand the transformation
We need to find the standard deviation of the transformed random variable 1−4X. The transformation can be expressed as:
Y=1−4X
where Y is the new random variable.
Step 2: Recall the properties of variance
The variance of a transformed variable AX+B is given by:
Var(AX+B)=A2⋅Var(X)
where A is a constant multiplier, and B is a constant added to the variable.
Step 3: Identify A and B
In our case:
- A=−4 (the coefficient of X)
- B=1 (the constant added)
Step 4: Calculate the variance of X
Given that σ(X)=2.6, we can find the variance of X:
Var(X)=σ2(X)=(2.6)2=6.76
Step 5: Apply the variance transformation formula
Now we apply the variance transformation formula:
Var(Y)=(−4)2⋅Var(X)=16⋅6.76
Step 6: Calculate the variance of Y
Now we compute:
Var(Y)=16⋅6.76=108.16
Step 7: Find the standard deviation of Y
The standard deviation of Y is the square root of the variance:
σ(Y)=√Var(Y)=√108.16
Step 8: Calculate the final result
Calculating the square root:
σ(Y)=10.4
Thus, the value of σ(1−4X) is 10.4.
Final Answer:
σ(1−4X)=10.4
We need to find the standard deviation of the transformed random variable 1−4X. The transformation can be expressed as:
Y=1−4X
where Y is the new random variable.
The variance of a transformed variable AX+B is given by:
Var(AX+B)=A2⋅Var(X)
where A is a constant multiplier, and B is a constant added to the variable.
In our case:
- A=−4 (the coefficient of X)
- B=1 (the constant added)
Given that σ(X)=2.6, we can find the variance of X:
Var(X)=σ2(X)=(2.6)2=6.76
Now we apply the variance transformation formula:
Var(Y)=(−4)2⋅Var(X)=16⋅6.76
Now we compute:
Var(Y)=16⋅6.76=108.16
The standard deviation of Y is the square root of the variance:
σ(Y)=√Var(Y)=√108.16
Calculating the square root:
σ(Y)=10.4
σ(1−4X)=10.4
Topper's Solved these Questions
- BOOK - MTG-WBJEECHAPTER - STATISTICS AND PROBABILITYEXERCISE - WB JEE Previous Years Questions ( CATEGORY 2 : Single Option Correct Type ( 2 Marks) )7videos
STATISTICS AND PROBABILITY
- BOOK - MTG-WBJEECHAPTER - STATISTICS AND PROBABILITYEXERCISE - WB JEE Previous Years Questions ( CATEGORY 3 : One or More than One Option Correct Type ( 2 Marks) )3videos
STATISTICS AND PROBABILITY
- BOOK - MTG-WBJEECHAPTER - STATISTICS AND PROBABILITYEXERCISE - WB JEE WORKOUT ( CATEGORY 3 : One or More than One Option Correct Type ( 2 Marks) )15videos
STATISTICS AND PROBABILITY
- BOOK - MTG-WBJEECHAPTER - SOLUTION OF TRIANGLESEXERCISE - WB JEE (Previous Years Questions) CATEGORY 2: Single Option Correct Type1videos
SOLUTION OF TRIANGLES
- BOOK - MTG-WBJEECHAPTER - STRAIGHT LINESEXERCISE - WB JEE Previous Years Questions28videos
STRAIGHT LINES
Similar Questions
Knowledge Check
- Question 1 - Select One
For a random variable X, if E(X) = 5 and V(X) = 6, then E(X2) is equal to
A19B31C61D11 - Question 2 - Select One
If the probability density function of a random variable X is f(x)=π2 in 0≤x≤2, then P(X>1.5X>1) is equal to
A716B34C712D2164 - Question 3 - Select One
If f(x)=k2x is a probability distribution of a random variable X that can take on the values x=0,1,2,3,4. Then , k is equal to
A1615B1516C3116DNone of these
Let X be a random variable with distribution.
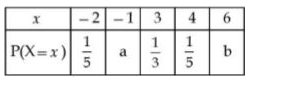
If the mean of X is 2.3 and variance of X is σ2, then 100σ2 is equal to :View SolutionTwo random variables are such that σX+Y>σX−Y, then r (X, Y) is positive.
View SolutionThe probability distribution of the random variable X is given by
Then, the value of V(X) is equal to
 View Solution
View SolutionIf random variable X~B(n=5,P=13), then P(2<X<4) is equal to
View SolutionFor the random variable X , if V(X) = 4 , E(X) = 3 , then E(X2) is …
View Solution