In a ABC,A≡(α,β),B≡(1,2),C≡(2,3), point A lies on the line y=2x+3, where α,β are integers, and the area of the triangle is S such that [S]=2 where [ .] denotes the greatest integer function. Then the possible coordinates of A can be (A) (−7,−11) (B) (−6,−9) (C)(2,7) (D) (3,9)Solution in Bengali
(−7,−11)
(−6,−9)
(2,7)
(3,9)
The correct Answer is:A, B, C, D
The point A(α,β) lies on y=2x+3.
Hence,
β=2α+3
A=(α,2α+3)
Area of ΔABC is ∣∣
∣∣12∣∣
∣∣α2α+31121231∣∣
∣∣∣∣
∣∣
=∣∣∣12[α(2−3)+(2α+3)(2−1)+1(3−4)]∣∣∣
=12|−α+2α+3−1|=12|α+2|=S
[S]=2or2≤S<3
therfore2≤12|α+2|<3
4≤|α+2|<6
|α+2|≤6
or −6≤α+2≤6
or −8≤α≤4
and |α+2|≥4
i.e., α+2≥4orα+2≤−4
i.e., α≥2orα≤−6
From (1) and (2) , we get
−8<α<−6or2≤α<4
or α=−7,−6,2,3
The possible coordiantes of A are (−7,−11),(−6,−9),(2,7) and (3,9). 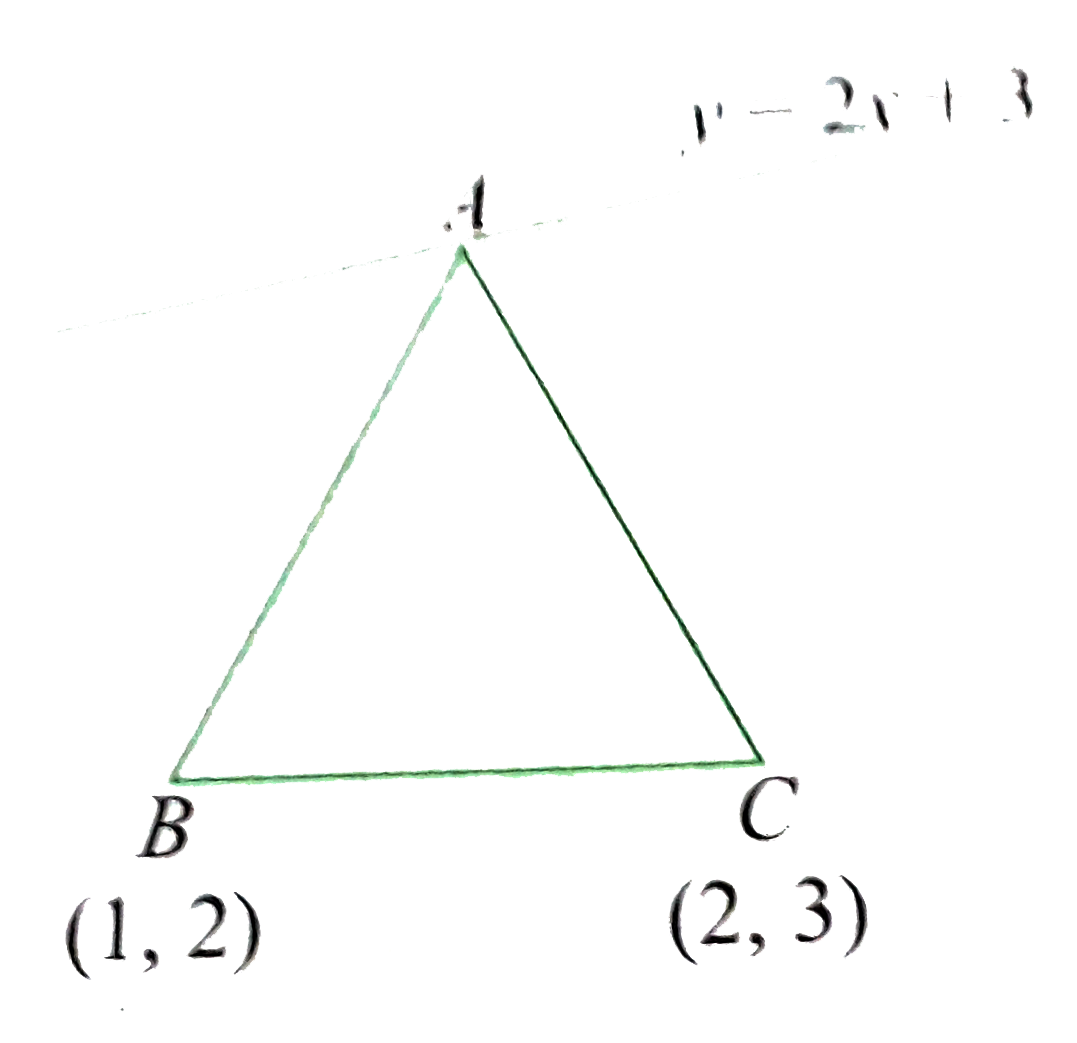
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Linked
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Exercises
59 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
For points P=(x1,y1)and Q=(x2,y2) of the co-ordinate plane a new distance d(P,Q)=|x1−x2|+|y1−y2| is defined .Let O(0,0)and A(3,2). The set of points in first quadrant which are equidistant from O and A is
View SolutionConsider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionThrough the point P(α,β) , where αβ>0, the straight line xa+yb=1 is drawn so as to form a triangle of area S with the axes. If ab>0, then the least value of S is αβ (b) 2αβ (c) 3αβ (d) none
View SolutionIn a ABC,A≡(α,β),B≡(1,2),C≡(2,3), point A lies on the line y=2x+3, where α,β are integers, and the area of the triangle is S such that [S]=2 where [ .] denotes the greatest integer function. Then the possible coordinates of A can be (a)(−7,−11) (b) (−6,−9) (c)(2,7) (d) (3,9)
View SolutionIn a triangle ABC,A=(α,β)B=(2,3),andC=(1,3). Point A lies on line y=2x+3, where α∈I. The area of ABC, , is such that [Δ]=5 . The possible coordinates of A are (where [.] represents greatest integer function). (a)(2,3) (b) (5,13) (−5,−7) (d) (−3,−5)
View SolutionIf αandβ are roots of the quadratic equation ax2+bx+c=0 and a+b+c>0,a−b+c>0&c<0,then[α]+[β] is equal to (where [.] denotes the greatest integer function) 10 b. −3 c. −1 d. 0
View SolutionIn a ΔABC,A≡(α,β),B≡(1,2),C≡(2,3) and point A lies on the line y = 2 x + 3 where α,β∈l. If the area of ΔABC be such that [Δ]=2, where [.] denotes the greatest integer function, find all possible coordinates of A.
View SolutionShow that lines.
x−a+dα−δ=y−aα=z−a−dα+δandx−b+cβ−λ=y−bβ=z−b−cβ+λ are coplanar.
View SolutionLet a, b, c ∈ R and α,β are the real roots of the equation ax2 + bx + c = 0 and if a + b + c < 0, a – b + c < 0 and c > 0 then [α]+[β] is equal to (where [.] denotes the greatest integer function.)
View SolutionLet a,b,cεR and α,β, are the real roots of the equation ax2+bx+c=0 and in a+b+c<0,a−b+c<0 andc>0 then [α]+[β] is equal to (where[.] denotes the greatest integer function).
View SolutionShow that the lines x−a+dα+δ=y−aα=z−a−dα+δ and x−b+cβ+γ=y−bβ=z−b−cβ+γ are coplanar.
View SolutionIn a ABC,A≡(α,β),B≡(1,2),C≡(2,3), point A lies on the line y=2x+3, where α,β are integers, and the area of the triangle is S such that [S]=2 where [ .] denotes the greatest integer function. Then the possible coordinates of A can be (−7,−11) (−6,−9) (2,7) (3,9)
View SolutionIn a triangle ABC,A=(α,β)B=(2,3),andC=(1,3). Point A lies on line y=2x+3, where α∈I. The area of ABC, , is such that [Δ]=5 . The possible coordinates of A are (where [.] represents greatest integer function). (a)(2,3) (b) (5,13) (−5,−7) (d) (−3,−5)
View Solution
