In a $A B C, A D$ is the altitude from $A$ such that $A D$ = 12 cm. $B D$ = 9 cm and $D C$ = 16 cm. Examine if $A B C$ is right angled at $A$ .

Video Solution

Answer

Step by step video & image solution for In a A B C ,\ A D is the altitude from A such that A D = 12 cm. B D = 9 cm and D C = 16 cm. Examine if A B C is right angled at A . by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.

Updated on:21/07/2023

Class 7 MATHS THE TRIANGLE AND ITS PROPERTIES

Topper's Solved these Questions

BOOK - RD SHARMACHAPTER - PROFIT AND LOSSEXERCISE - All Questions
51videos
PROFIT AND LOSS
BOOK - RD SHARMACHAPTER - RATIO AND PROPORTIONEXERCISE - All Questions
79videos
RATIO AND PROPORTION

Knowledge Check

Question 1 - Select One
In a $Δ A B C$ right angled at B, D is a point on AC such that BD is an angle bisector of B. If AD = 12 cm, CD = 16 cm then find the perimeter of triangle ABC.
A49.6 cm
B67.2 cm
C56.4 cm
D48 cm

In Figure, $B D$ and $C E$ are two altitudes of a $A B C$ such that $B D = C E .$ Prove that $A B C$ is isosceles.

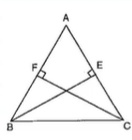View Solution
In Fig.42, $A B C D$ is a parallelogram in which $A D = 21 c m,$ $D H = 18 c m$ and $D K = 27 c m .$ The length of side $A B$ is 63 cm (b) 63.5 cm 31.5 cm (d) 31 cm
View Solution
In $A B C, ∠ A = 90^{0} a n d A D$ is an altitude. Complete the relation $\frac{B D}{D A} = \frac{A B}{()}$ .
View Solution
In a $A B C$ , perpendicular $A D$ from $A$ on $B C$ meets $B C$ at $D$ . If $B D = 8 c m$ , $D C = 2 c m$ and $A D = 4 c m$ , then $A B C$ is isosceles (b) $A B C$ is equilateral (c) $A C = 2 A B$ (d) $A B C$ is right-angled at $A$ .
View Solution
In Fig.42, $A B C D$ is a parallelogram in which $A D = 21 c m, D H = 18 c m$ and $D K = 27 c m .$ The perimeter of the parallelogram is 105 cm (b) 84.5 cm 169 cm (d) 52.5 cm
View Solution
In a right-angled triangle ABC, D is the foot of the perpendicular from B on the hypotenuse AC. If AB = 3 cm and BC = 4 cm, what is the area of $△ A B D$ ?
(a) 54 cm
(b) 54/29 cm
(c) 54/23 cm
(d) None of these
View Solution
If $A B C D E F$ such that $D E = 3 c m$ , $E F = 2 c m$ , $D F = 2.5 c m$ , $B C = 4 c m$ , then perimeter of $A B C$ is (a) 18cm (b) 20cm (c) 12cm (d) 15cm
View Solution

RD SHARMA-PROPERTIES OF TRIANGLES-All Questions

Verity that the following numbers represent Pythagorean triplet: 27...
01:37
In A B C ,\ /A B C=100^0,\ /B A C=35^0\ \ a n d\ B D|A C meets side A ...
02:43
In a A B C ,\ A D is the altitude from A such that A D = 12 cm. B D = ...
04:20
Draw a triangle A B C , with A C=4\ c m ,\ B C=3\ c m\ a n d\ /C=105^0...
02:56
Draw a triangle A B C , with A C=4\ c m ,\ B C=3\ c m\ a n d\ /C=80^0d...
02:33
If the measure of the angle of a triangle are (2x)^0,\ (3x-5)^0 and...
01:15
The angles of a triangle are in the ratio 2:3: 7. The measure of th...
01:41
In a A B C ,\ If 2/A=3\ /B=6\ /C , then the measure of the smalle...
02:11
In a A B C , if /A+/B=150^0 and /B+/C=75^0, then /B= 35^0 (b) 45^0 ...
01:48
In a A B C , if /A-/B=33^0 and /B-/C=18^0, then /B= 35^0 (b) 45^0 ...
01:50
If the measure of the angles of a triangle are (2x-5)^0,(3x-1/2)\ a...
01:36
In Fig. 59, the value of x\ is 84 (b) 74 (310)/9 (d) (301)/9
01:24
In Fig.60, the value of x\ a n d\ y are x=20 ,\ y=130\ (b) x=40 ,\ y...
02:04
In Fig.61, the value of x is 72^0 (b) 50 58 (d) 48
01:41
In Fig.62, if A B D E , then the value of x is 25 (b) 35 40 (d) 45
02:42
In Fig.63, if A B C D , the value of x is 25 (b) 35 15 (d) 20
01:55
In Fig.64, if A B C D , the values of x\ a n d\ y are x=21 ,\ y=28 (...
03:02
In Fig.65, if A B C E ,\ then the values of x\ a n d\ y\ are x=26 ,...
02:37
In Fig.66, if A F D E ,\ then x= 37 (b) 57 47 (d) 67
02:11
In Fig.67, the value of x\ a n d\ y\ a r e x=130 ,\ y=120 (b) x=120 ...
02:03

Home
Ask Doubt
Profile

In aABC, AD is the altitude from A such that AD = 12 cm. BD = 9 cm and DC = 16 cm. Examine ifABC is right angled at A .

Topper's Solved these Questions

Similar Questions

Knowledge Check

In a ΔABC right angled at B, D is a point on AC such that BD is an angle bisector of B. If AD = 12 cm, CD = 16 cm then find the perimeter of triangle ABC.

RD SHARMA-PROPERTIES OF TRIANGLES-All Questions

In a $A B C, A D$ is the altitude from $A$ such that $A D$ = 12 cm. $B D$ = 9 cm and $D C$ = 16 cm. Examine if $A B C$ is right angled at $A$ .

In a $Δ A B C$ right angled at B, D is a point on AC such that BD is an angle bisector of B. If AD = 12 cm, CD = 16 cm then find the perimeter of triangle ABC.