If ABCDEF such that DE=3cm , EF=2cm , DF=2.5cm , BC=4cm , then perimeter of ABC is (a) 18cm (b) 20cm (c) 12cm (d) 15cm
To find the perimeter of triangle ABC given that it is similar to triangle DEF, we can follow these steps:
1. Identify the given lengths:
- DE=3cm
- EF=2cm
- DF=2.5cm
- BC=4cm
2. Set up the ratios for similar triangles:
Since triangles ABC and DEF are similar, the ratios of corresponding sides are equal:
ABDE=BCEF=ACDF
3. Calculate the ratio using the known lengths:
From the ratio BCEF:
BCEF=42=2
4. Use the ratio to find AB:
Since ABDE=2:
AB3=2⟹AB=2×3=6cm
5. Use the ratio to find AC:
Since ACDF=2:
AC2.5=2⟹AC=2×2.5=5cm
6. Calculate the perimeter of triangle ABC:
The perimeter P is given by:
P=AB+BC+AC
Substituting the values we found:
P=6+4+5=15cm
Final Answer:
The perimeter of triangle ABC is 15cm. Thus, the correct option is (d) 15 cm.
---
- DE=3cm
- EF=2cm
- DF=2.5cm
- BC=4cm
Since triangles ABC and DEF are similar, the ratios of corresponding sides are equal:
ABDE=BCEF=ACDF
From the ratio BCEF:
BCEF=42=2
Since ABDE=2:
AB3=2⟹AB=2×3=6cm
Since ACDF=2:
AC2.5=2⟹AC=2×2.5=5cm
The perimeter P is given by:
P=AB+BC+AC
Substituting the values we found:
P=6+4+5=15cm
The perimeter of triangle ABC is 15cm. Thus, the correct option is (d) 15 cm.
Topper's Solved these Questions
Similar Questions
ABC is such that AB=3cm , BC=2cm and CA=2.5cm . If DEF~ABC and EF=4cm , then perimeter of DEF is (a) 7.5cm (b) 15cm (c) 22.5cm (d) 30cm .
View SolutionABCDEF , ar(ABC)=9cm2 , ar(DEF)=16cm2 . If BC=2.1cm , then the measure of EF is 2.8cm (b) 4.2cm (c) 2.5cm (d) 4.1cm
View SolutionIn an isosceles triangle ABC , if AB=AC=25cm and BC=14cm , then the measure of altitude from A on BC is (a) 20cm (b) 22cm (c) 18cm (d) 24cm
View SolutionIn Fig. 10.98, a circle touches the side DF of EDF at H and touches ED and EF produced at K and M respectively. If EK=9cm , then the perimeter of EDF is (FIGURE) (a) 18cm (b) 13.5cm (c) 12cm (d) 9cm
View SolutionABCDEF . If BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)= 108cm2 (b) 96cm2 (c) 48cm2 (d) 100cm2
View SolutionIn Fig. 10.97, the sides AB, BC and CA of triangle ABC , touch a circle at P, Q and R respectively. If PA=4cm , BP=3cm and AC=11cm , then length of BC is (FIGURE) (a) 11cm (b) 10cm (c) 14cm (d) 15cm
View SolutionABCD is a trapezium in which ABDC. If ar(ABD)=24 cm2and AB=8 cm, then height of ABC is 3 cm (b) 4 cm (c) 6 cm (d) 8 cm
View SolutionIn Fig.42, ABCD is a parallelogram in which AD=21 cm, DH=18 cm and DK=27 cm. The perimeter of the parallelogram is 105 cm (b) 84.5 cm 169 cm (d) 52.5 cm
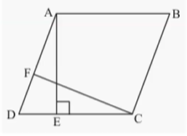
View SolutionIn Figure, ABCD is a parallelogram. If AB=12cm,AE=7.5cm,CF=15cm, then AD=
(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
View SolutionIf ABC and DEF are two triangles such that ABDE=BCEF=CAFD=25 , then Area(ABC):Area(DEF)= 2:5 (b) 4:25 (c) 4:15 (d) 8:125
View Solution
