Question

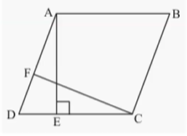
In $ABC,E$
is the mid-point of
median $AD$
such that $BE$
produced meets $AC$
at $F\stackrel{.}{}$
If $AC=10.5CM,$
then $AF=$

3cm (b)
3.5cm (c) 2.5cm (d) 5cm

Explanation

Given : In `triangleABC`, E is the mid -point of median AD such that BE produced meets AC at F. Also, AC = 10.5 cm.

Cons. : Draw `DG|\| AF`

In `triangleADG`, E is mid -point of `AD` and `EF|\| DG`

`therefore` `F` is mid -point of `AG`

`AF=FG`____1

In `triangleBCF`, `D` is mid -point of `BC` and `DG|\| BF`

`therefore` `G` is mid -point of `FC`

`FG=GC`

From 1 and 2

`AF=FG=GC=1/3AC`

Now, `AC=10.5 cm`

So, `AF=1/3xx10.5=3.5`cm

Hence, option (b) is correct.