In ABC Prove that AB2+AC2=2(AO2=2(AO2+BO2) , where O is the middle point of BCSolution in Bengali
Let point B and C lie on the x-axis such that BD=DC, where, D(0,0) is midpoint of BC.
Let point A be (x,y).
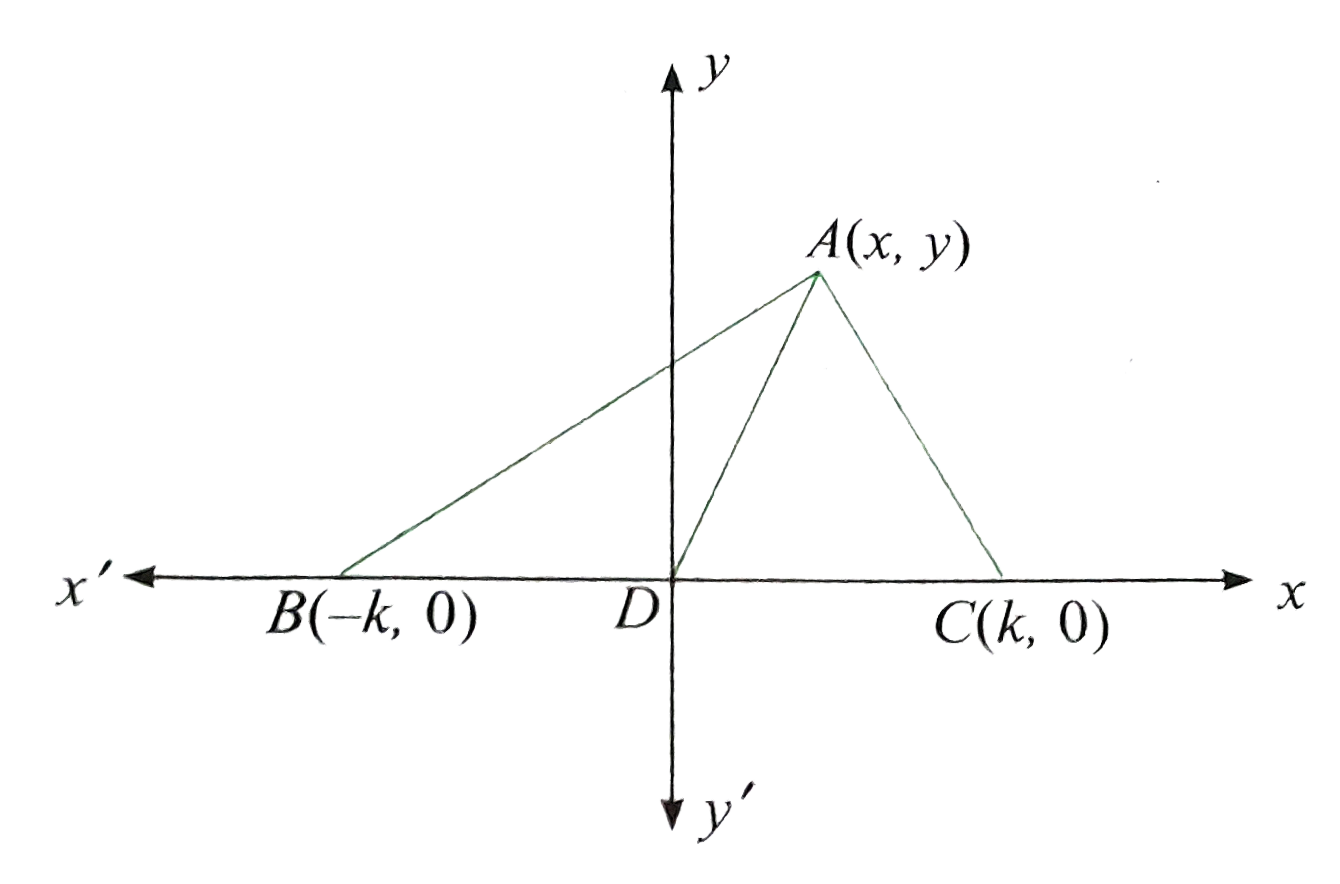
BD=k.So, point B is (−k,0) and point C is (k,0).
Now, AB2+AC2=(x+k)2+(y−0)2+(x−k)2+(y−0)2
=x2+k2+2xk+y2+x2k2−2xk+y2
=2x2+2y2+2k2=2(x2+y2+k2)
And 2(AD2+BD2)=2[(x−0)2+(y−0)2+k2]
=2(x2+y2+k2)
Therefore, AB2+AC2=2(AD2+BD2)
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.111videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.121videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.91videos
COORDINATE SYSYEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Find the coordinates of the circumcenter of the triangle whose vertices are (A(5,−1),B(−1,5), and C(6,6). Find its radius also.
04:35View SolutionTwo points O(0,0) and A(3,√3) with another point P form an equilateral triangle. Find the coordinates of P.
02:10View SolutionIf θ is an angle by which axes are rotated about origin and equation ax2+2hxy+by2=0 does not contain xy term in the new system, then prove that tan2θ=2ha−b.
02:22View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
05:16View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
06:58View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2
 01:41View Solution
01:41View SolutionABCD IS A PARALLELOGRAM AND O is any point in its interior. Prove that: ar (AOB)+ ar (COD)= ar (BOC)+ ar(AOD) ar (AOB)+ar (COD)=12 ar(^(gm)ABCD) Given: A parallelogram ABCD and O is a point in its interior. To Prove: ar ( AOB)+ ar(COD)=ar (BOC)+ar(AOD)
01:55View SolutionA+H_(2)O to B+HCl B+H_(2)O to C+HCl Compound (A), (B) and (C) will be respectively:
01:11View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
07:30View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
 07:06View Solution
07:06View SolutionIf B is an idempotent matrix, and A=I−B, then a. A2=A b. A2=I c. AB=O d. BA=O
02:44View SolutionIn ABC Prove that AB2+AC2=2(AO2+BO2) , where O is the middle point of BC
10:48View SolutionIf 2→AC = 3→CB , then prove that 2→OA =3→CB then prove that 2→OA + 3→OB =5→OC where O is the origin.
02:11View SolutionFrom a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
06:14View SolutionA point O in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D . Prove that OB2+OD2=OC2+OA2
02:12View SolutionIn a quadrilateral ABCD , ∠B=90o , AD2=AB2+BC2+CD2 , prove that ∠ACD=90o
04:22View Solution

