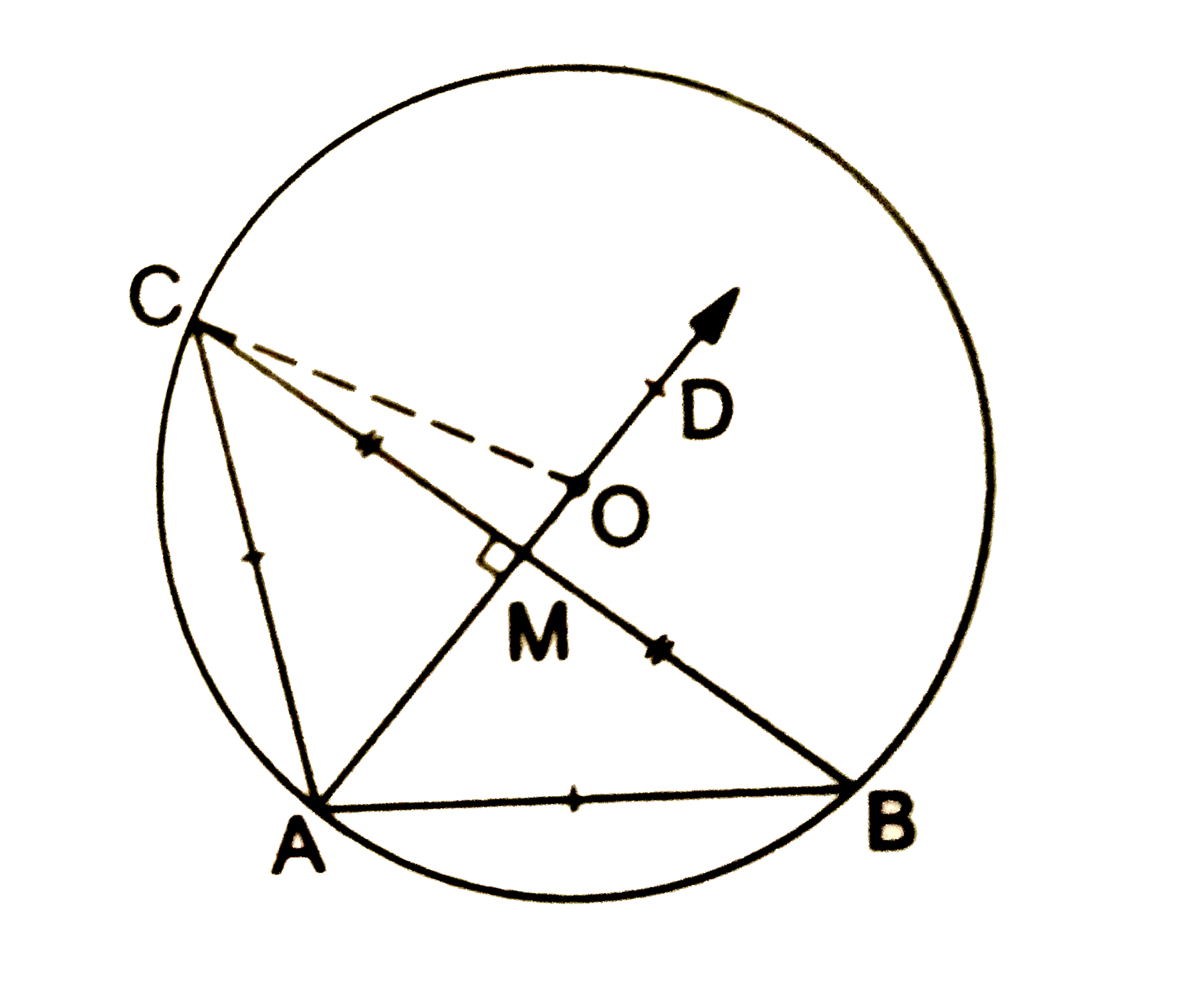
In a circle of radius $5 c m, A B a n d A C$ are two chords such that $A B = A C = 6 c m$ .
Find the length of the chord $B C$

Video Solution

Text Solution

Verified by Experts

Let $A D$ be the bisector of $∠ B A C .$
Then , $A D$ is the perpendicular bisector of $B C$ and passes through the centre $O$ . Join $C O$
Let $A D$ meet $B C$ in $M .$
Then , $B M$ $=$ $C M .$
From the right $Δ A M C,$ we have
$M C^{2} = A C^{2} - A M^{2} = 36 c m^{2} - A M^{2}$ ....(i)
From the right $Δ O M C$ , we have
$M C^{2} = O C^{2} - O M^{2} = 25 c m^{2} - {(O A - A M)}^{2}$
$= 25 c m^{2} - {(5 c m - A M)}^{2}$ ....(ii)
$∴ 36 c m^{2} - A M^{2} = 25 c m^{2} = - {(5 c m - A M)}^{2}$ [from (i) and (ii) ]
$\Rightarrow 36 c m^{2} - A M^{2} = 25 c m^{2} - (25 c m^{2} - A M^{2} + 10 \times A M)$
$\Rightarrow 36 c m^{2} - A M^{2} = 25 c m^{2} - 25 c m^{2} - A M^{2} + 10 c m \times A M$
$\Rightarrow 36 c m^{2} = 10 \times A M$
$\Rightarrow A M = 3.6 C M$ .
$∴ M C = \sqrt{36 - {(3.6)}^{2}} c m = \sqrt{23.04} c m = 4.8 c m$
$∴ B C = 2 \times M C = 9.6 c m$

Updated on:21/07/2023