In a circle with centre O, a tangent is drawn from an external point A to the circel which touches the circel at B. If OB = 5 cm, OA =13 cm, then the length of AB= Solution in Bengali
12 cm
13 CM
6.5cm
6 cm
In the circel with centre O, AB is a tangent and OB is a radius passing throgh point of contact.
∴OB⊥AB,∴∠OBA=90∘
∴ΔAOB is a right-angaled triangle, of which OA is the hypotensius.
∴OB2+AB2=OA2[bypythagoras'theorem]
or 52+AB2=132[∵OB=5cm,OA=13cm]
or25+AB2=169or,AB2=169−25
or AB2=144or,AB=√144or,AB=12
Hence the length of AB = 12 cm
∴ (a) is correct.

Topper's Solved these Questions
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.120videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.223videos
THEOREMS RELATED TO TANGENT IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXERCISE 2.3 (Long Answer Type Questions)14videos
THEOREMS RELATED TO ANGLES IN A CIRCLE
- BOOK - CALCUTTA BOOK HOUSECHAPTER - TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES EXERCISE - EXERCISE66videos
TRIGONOMETRIC RATIOS AND TRIGONOMETRIC IDENTITIES
Similar Questions
PR and PS are two tangents drawn from a extental point P of the Circle with centre at O. If PR=8cmand∠RPO=60∘, then the length of PS=
02:22View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
04:04View SolutionProve that angle in the segment of a circle which is greater than a semi-circle is an acute angle.
02:29View SolutionIf tanθ=pq, what is the value of psecθ−q cosecθpsecθ+q cosecθ=
06:42View SolutionFrom a point P which is at a distance of 13 cm form the centre of the circle of radius 5 cm, a tangent is drawn to the circle . The length of the tangent is ____________
02:02View SolutionIn the figure, point P is the centre of the circle and line AB is the tangent to the circle at the point T. The radius of the circle is 6 cm . Find PB, if ∠TPB=60∘
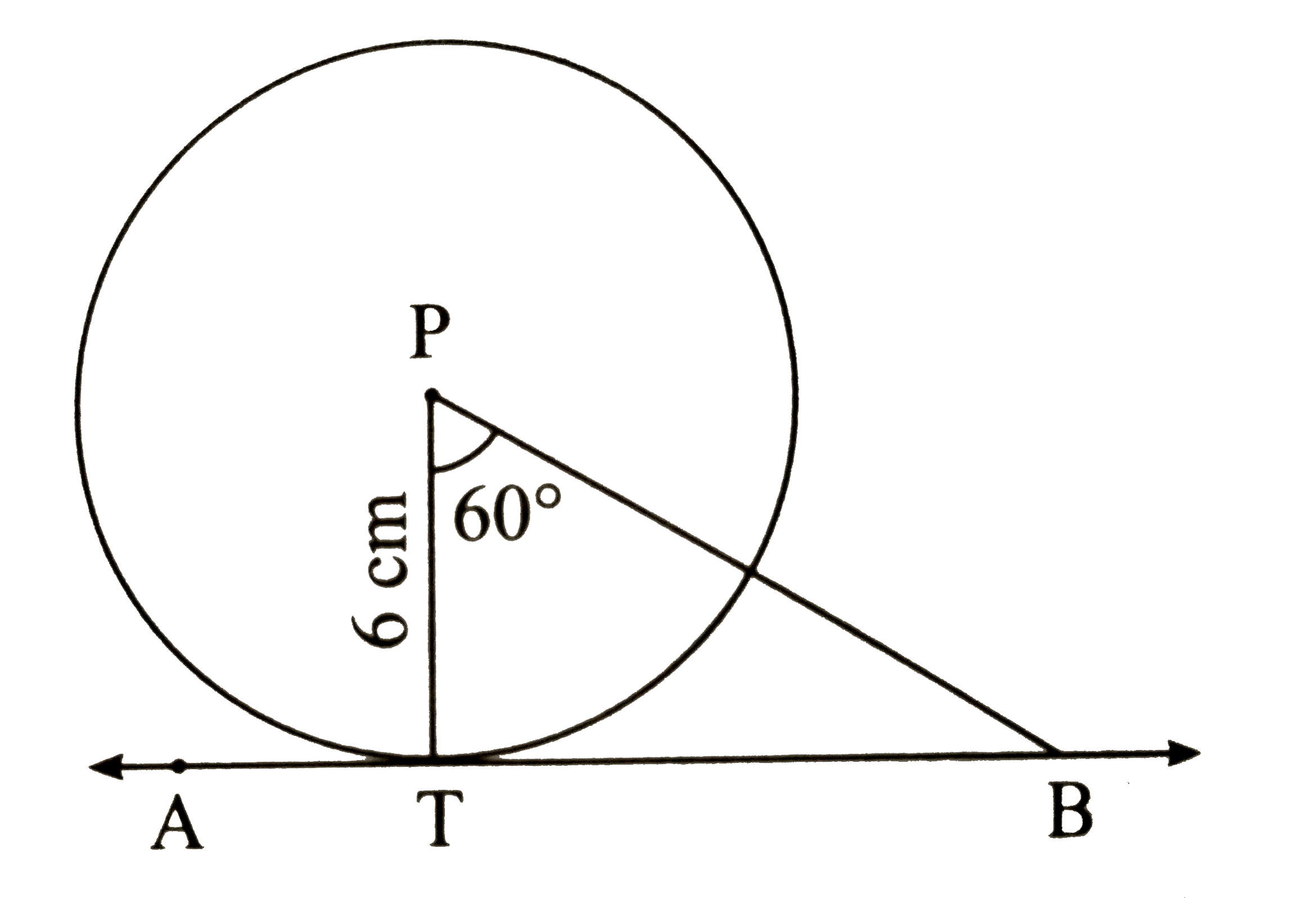 03:09View Solution
03:09View SolutionA tangent AB, at a point A of a circle of radius 5 cm, meets a line through the centre O at point B such that OB =12 cm. Length AB is
02:35View SolutionThe length of radius of a circel with centre O is 5 cm. P is a point at a distacne of 13 cm from the point O. PQ and PR are two tangensts from the point P to the circles, the area of the quadrilaterals PQOR is
03:02View SolutionThe lengths of radii of two circels are 3.5cmand2cm. They touch each other internally. The distance between the centres of the circels is
02:18View SolutionIn the adjoining figure, two tangents drawn from external point C to a circle with centre O touches the circel at the point P and Q respectively. A tangent drawn at another point R of the circle intersects CP and CQ at the points A and B respectively. If CP = 7 cm and BC =11 cm, then determine the length of BR.
03:59View SolutionThe tangent drawn from an extenral point A of the circle with centre C touches the circle at B. If BC=5cm,AC=13 cm, then the length of AB=
02:47View SolutionThe radius of a circle with centre O is 5 cm. The length of the tangent to the circle from the external point is 12 cm. Find the distance of that point from the centre.
02:02View SolutionFind the length of tangent segment drawn to a circle with radius 5 cm from a point 13 cm from the centre of the circle.
02:37View SolutionIn the given figure, O is the centre of the circle. AB is tangent. AB=12cmandOB=13cm. Find OA:
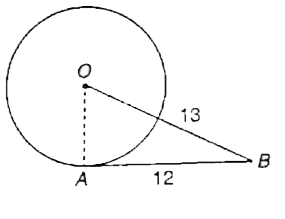 02:48View Solution
02:48View SolutionFind the length of a tangent drawn to a circle with radius 5 cm, from a point 13 cm from the centre of the circle.
03:43View Solution

