In a class, there are 225 students. Which of the following cannot be the ratio of the number of sutdents passed to the number of students failed?
2:3
7:8
5:4
3:4
The correct Answer is:D
To solve the problem, we need to determine which of the given ratios cannot represent the number of students who passed to the number of students who failed in a class of 225 students.
1. Understand the Total Students:
We know that the total number of students in the class is 225.
2. Define the Ratio:
Let the ratio of students who passed to those who failed be represented as p:f. This means:
p+f=225
where p is the number of students who passed and f is the number of students who failed.
3. Express the Ratio in Terms of a Variable:
If we express the ratio p:f as a:b, we can write:
p=akandf=bk
where k is a common multiplier. Therefore, we have:
ak+bk=225⇒(a+b)k=225
This means that k can be calculated as:
k=225a+b
4. Check Each Option:
We need to check if a+b divides 225 evenly (i.e., k must be an integer).
- Option 1: Ratio 2:3
a+b=2+3=5⇒k=2255=45(integer)
- Option 2: Ratio 7:8
a+b=7+8=15⇒k=22515=15(integer)
- Option 3: Ratio 5:4
a+b=5+4=9⇒k=2259=25(integer)
- Option 4: Ratio 3:4
a+b=3+4=7⇒k=2257≈32.14(not an integer)
5. Conclusion:
The ratio that cannot represent the number of students who passed to those who failed is Option 4: 3:4.
We know that the total number of students in the class is 225.
Let the ratio of students who passed to those who failed be represented as p:f. This means:
p+f=225
where p is the number of students who passed and f is the number of students who failed.
If we express the ratio p:f as a:b, we can write:
p=akandf=bk
where k is a common multiplier. Therefore, we have:
ak+bk=225⇒(a+b)k=225
This means that k can be calculated as:
k=225a+b
We need to check if a+b divides 225 evenly (i.e., k must be an integer).
a+b=2+3=5⇒k=2255=45(integer)
- Option 2: Ratio 7:8
a+b=7+8=15⇒k=22515=15(integer)
- Option 3: Ratio 5:4
a+b=5+4=9⇒k=2259=25(integer)
- Option 4: Ratio 3:4
a+b=3+4=7⇒k=2257≈32.14(not an integer)
The ratio that cannot represent the number of students who passed to those who failed is Option 4: 3:4.
Topper's Solved these Questions
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - LEVEL 219videos
RATIO, PROPORTION AND VARIATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - LEVEL 36videos
RATIO, PROPORTION AND VARIATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - RATIO, PROPORTION AND VARIATIONEXERCISE - Essay Type Question5videos
RATIO, PROPORTION AND VARIATION
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - PROFIT AND LOSS DISCOUNT AND PARTNERSHIP EXERCISE - CONCEPT APPLICATION (LEVEL 2)29videos
PROFIT AND LOSS DISCOUNT AND PARTNERSHIP
- BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - REAL NUMBERS AND LCM AND HCF EXERCISE - level -111videos
REAL NUMBERS AND LCM AND HCF
Similar Questions
Direction: There are 1250 total students in 5 different classes in a school. The number of students in class I is 50 less than the number of students in class II. The number of class IV students is 50 more than the number of students in class II. The average number of students in class III and class V is 250. The number of students in class III is 10% less than the number of students in class I.
The ratio of the total number of students of class V to the total number of students of class III isView Solution100 students appeared in annual exami-nation. 60 students passed. The ratio of the number of students who failed to the total number of students is
View Solution
Knowledge Check
- Question 1 - Select One
In a class, there are 225 students. Which of the following cannot be the ratio of the number of sutdents passed to the number of students failed?
A2:3B7:8C5:4D3:4
Direction: There are 1250 total students in 5 different classes in a school. The number of students in class I is 50 less than the number of students in class II. The number of class IV students is 50 more than the number of students in class II. The average number of students in class III and class V is 250. The number of students in class III is 10% less than the number of students in class I.
The total number of students of class IV and the number of students of class II isView SolutionDirection: There are 1250 total students in 5 different classes in a school. The number of students in class I is 50 less than the number of students in class II. The number of class IV students is 50 more than the number of students in class II. The average number of students in class III and class V is 250. The number of students in class III is 10% less than the number of students in class I.
The number of students of class V is what percent of the total number of students?View SolutionDirection: There are 1250 total students in 5 different classes in a school. The number of students in class I is 50 less than the number of students in class II. The number of class IV students is 50 more than the number of students in class II. The average number of students in class III and class V is 250. The number of students in class III is 10% less than the number of students in class I.
The average number of students of class II and class III isView SolutionDirection: There are 1250 total students in 5 different classes in a school. The number of students in class I is 50 less than the number of students in class II. The number of class IV students is 50 more than the number of students in class II. The average number of students in class III and class V is 250. The number of students in class III is 10% less than the number of students in class I.
The number of students of class I is -View SolutionOut of 30 students in a class, 20 like cricket and 10 like Hockey. The ratio of the number of students liking Hockey to the total number of students is
View SolutionDirection :- The following pie-chart shows the number of students who failed in different subjects in an examination. Examine the chart and answer the following questions. The total number of students who have failed is 500.

The number of students failed in Science is less than the number of student failed in all other subects byView SolutionThe following pie-chart shows the number of students who failed in different subjects in an examination. Examine the chart and answer the following questions. The total number of students who have failed is 500.
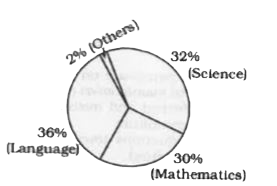
The number of students failed in science is less than the number of students failed in all other subjects by :View Solution

