In a classroom, 4 friends are seated at the points A. B. C and D as shown in Fig. 7.8. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, Don't you think ABCD is a square? Chameli disagrees. Using distance formula, find which of them is correct.
To determine whether the points A, B, C, and D form a square, we will use the distance formula. The distance formula between two points (x1,y1) and (x2,y2) is given by:
D=√(x2−x1)2+(y2−y1)2
Step 1: Identify the coordinates of points A, B, C, and D
Let's assume the coordinates of the points are as follows:
- A(3,4)
- B(6,7)
- C(9,4)
- D(6,1)
Step 2: Calculate the distance AB
Using the distance formula for points A and B:
AB=√(6−3)2+(7−4)2
=√32+32=√9+9=√18=3√2
Step 3: Calculate the distance BC
Now, calculate the distance between points B and C:
BC=√(9−6)2+(4−7)2
=√32+(−3)2=√9+9=√18=3√2
Step 4: Calculate the distance CD
Next, calculate the distance between points C and D:
CD=√(6−9)2+(1−4)2
=√(−3)2+(−3)2=√9+9=√18=3√2
Step 5: Calculate the distance DA
Finally, calculate the distance between points D and A:
DA=√(3−6)2+(4−1)2
=√(−3)2+32=√9+9=√18=3√2
Step 6: Compare the distances
We have found that:
- AB=3√2
- BC=3√2
- CD=3√2
- DA=3√2
Since all four sides are equal, we can conclude that the quadrilateral formed by points A, B, C, and D is indeed a square.
Conclusion
Champa was correct in saying that ABCD is a square.
---
Let's assume the coordinates of the points are as follows:
- A(3,4)
- B(6,7)
- C(9,4)
- D(6,1)
Using the distance formula for points A and B:
=√32+32=√9+9=√18=3√2
Now, calculate the distance between points B and C:
=√32+(−3)2=√9+9=√18=3√2
Next, calculate the distance between points C and D:
=√(−3)2+(−3)2=√9+9=√18=3√2
Finally, calculate the distance between points D and A:
=√(−3)2+32=√9+9=√18=3√2
We have found that:
- AB=3√2
- BC=3√2
- CD=3√2
- DA=3√2
Champa was correct in saying that ABCD is a square.
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - EXERCISE 7.35videos
COORDINATE GEOMETRY
- BOOK - NCERT ENGLISHCHAPTER - COORDINATE GEOMETRYEXERCISE - SOLVED EXAMPLES15videos
COORDINATE GEOMETRY
- BOOK - NCERT ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - EXERCISE 11.27videos
CONSTRUCTIONS
- BOOK - NCERT ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - EXERCISE 8.37videos
INTRODUCTION TO TRIGONOMETRY
Similar Questions
When is the higher rate of energy being delivered to a light bulb higher : just after it is turned on, the glow of the filament is increasing, or after it has been on for a few seconds and the glow is steady ?
 View Solution
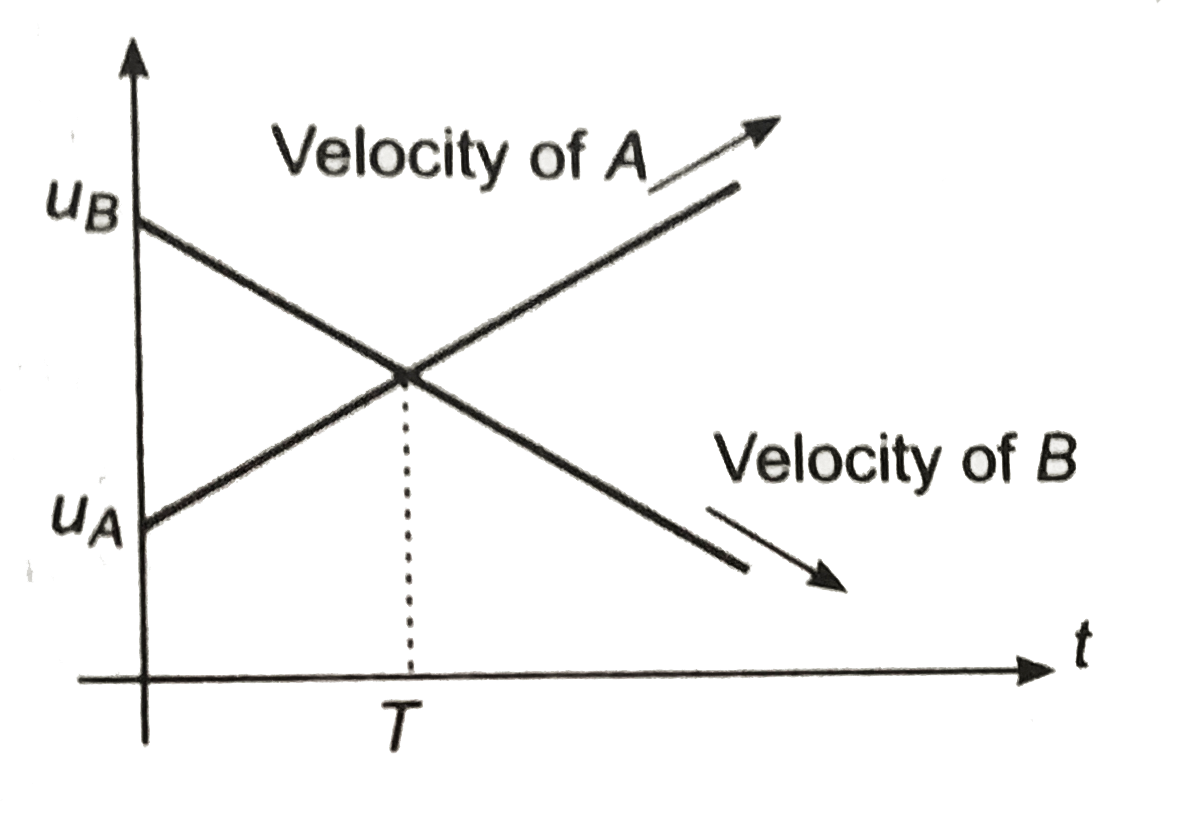
View SolutionA situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
7. After 10 s of the start of motion of both objects A and B, find the value of velocity of A if uA=6ms−1,uB=12ms−1 and at T velocity of A is 8ms−1andT=4s
 View Solution
View Solution
