Question

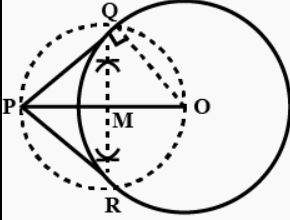
Draw a
circle of radius 6cm. From a point 10cm away from its centre, construct the
pair of tangents to the circle and measure their lengths.

Explanation

Steps of Construction:


1. A circle with a radius of 6 cm is drawn taking O as the centre.



2. Point P is marked at 10 cm away from the centre of the circle.


3. With the half of compass mark M which is the midpoint of OP.


4. Draw a circle with centre M, taking radius MO or MP which intersects the given circle at Q and R.


5. Now join PQ and PR. These are the tangents of the circle.


We know that the tangent to a circle is perpendicular to the radius through the point of contact.


∴ In △OPQ, OQ⊥QP
and in △OPR, OR⊥PR


Hence, both △OPQ and △OPR are right-angle triangles.


Applying Pythagoras theorem to both △s, we get:
`(OP)^2
=(OQ)^2+(PQ)^2`



and `(OP)^2 =(OR)^2
+(PR)^2`



`OQ=OR`=radius=6 cm and `OP=10` cm


∴ `10^2=6^2+(PQ )^2`


and `10^2=6^2+(PR)^2`



`⇒(PQ)^2
=100−36=64`


and `(PR)^2
=100−36=64`


then, `PQ=PR=8 cm`


Hence, the length of the tangents to a circle of radius 6 cm, from a point 10 cm away from the centre of the circle, is `8 cm.`