In a cyclic quadrilateral ABCD, prove that tan2B2=(s−a)(s−b)(s−c)(s−d),a,b,c,andd being the lengths of sides ABC, CD and DA respectively and s is semi-perimeter of quadrilateral. Solution in Punjabi
The correct Answer is:tan2B2=(s−a)(s−b)(s−d)(s−c)
Step by step video & image solution for In a cyclic quadrilateral ABCD, prove that tan ^(2)""(B)/(2)=((s-a)(s-b))/((s-c)(s-d)),a,b,c, and d being the lengths of sides ABC, CD and DA respectively and s is semi-perimeter of quadrilateral. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Match the statements of Column I with values of Column II.

View SolutionIn the given figure,if AB=AC,∠BAD=30∘andAE=AD, then x is equal to
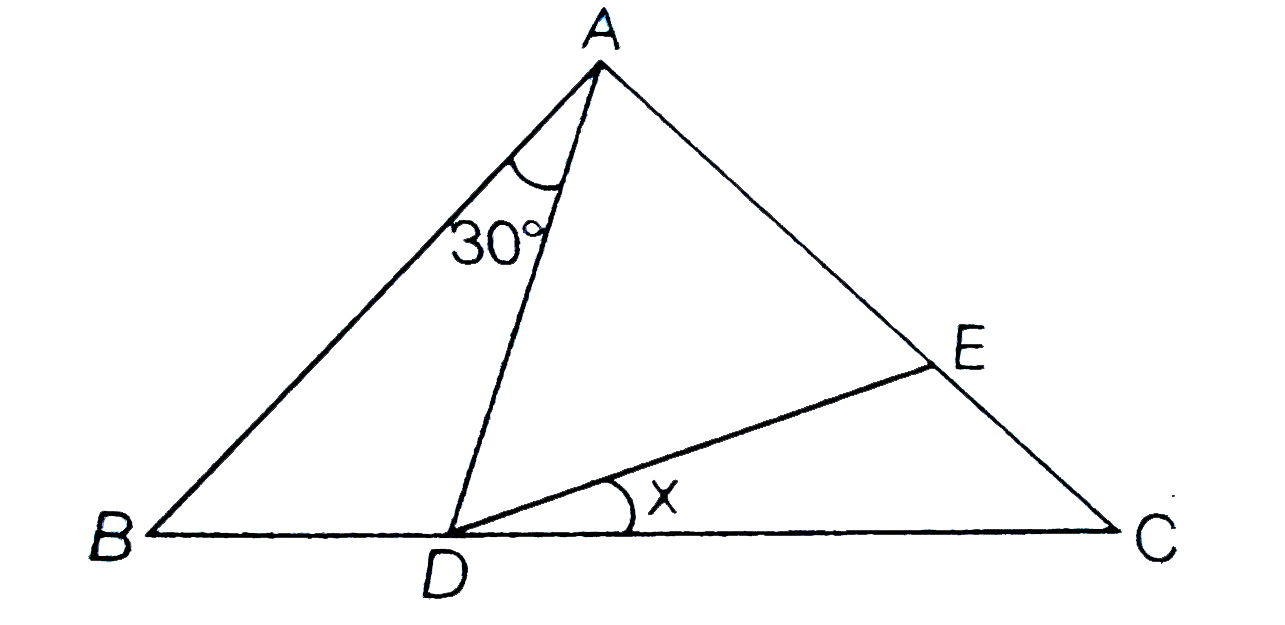
View SolutionLet O be the origin and let PQR be an arbitrary triangle. The point S is such that ¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OQ+¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OR⋅¯¯¯¯¯¯OP+¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OS=¯¯¯¯¯¯OQ⋅¯¯¯¯¯¯OR+¯¯¯¯¯¯OP⋅¯¯¯¯¯¯OS Then the triangle PQR has S as its
View SolutionLet a,b,c be in A.P. and |a|<1,|b|<1|c|<1.ifx=1+a+a2+....to ∞,y=1+b+b2+....to ∞and,z=1+c+c2+...to ∞, then x,y,z are in
View SolutionIf a,b,c are the sides of a triangle and s=(a+b+c)/(2), then prove that 8(s-a)(s-b)(s-c)<=abc
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minimum value of the sum of the lenghts of diagonals is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
When the perimeter is minimum, the quadrilateral is necessarily
View Solutionकिसी त्रिभुज ABC में सिद्ध कीजिए कि-
(s−a)tanA2=(s−b)tanB2=(s−c)tanC2
View SolutionSemi-perimeter (s) of triangle of side a,b,c is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minium perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
The minimum value of the sum of the lenghts of diagonals is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 2s=a+b++c+d,a,b,candd are the sides of the quadrilateral
Now consider a cyclic quadrilateral ABCD of area 1 sq. unit and answer the following question
When the perimeter is minimum, the quadrilateral is necessarily
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
The minimum perimeter of the quadrilateral is
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
The minimum value of the sum of the lengths of diagonals
View SolutionThe area of any cyclic quadrilateral ABCD is given by A2=(s−a)(s−b)(s−c)(s−d), where 28 = a + b + c + d, a, b,c and d are the sides of the quadrilateral. Now consier a cyclic quadrilateral ABCD of area 1sq.unit and answer the following questions:
When the perimeter is minimum, the quadrilateral is necessarily
View Solution
