In a cyclic trapezium ABCD, side AB is parallel to side DC. Prove that :
side AD = side BC.
To prove that in a cyclic trapezium ABCD with AB∥DC, the sides AD and BC are equal, we can follow these steps:
1. Identify the Given Information:
We are given a cyclic trapezium ABCD where AB is parallel to DC.
2. Draw the Figure:
Draw trapezium ABCD with AB parallel to DC. Label the points accordingly.
3. Use the Property of Parallel Lines:
Since AB∥DC, we can use the property of alternate interior angles. When we draw a transversal line AC, we have:
∠DCA=∠BAC
(Alternate interior angles are equal).
4. Relate Angles to Arcs:
The angles ∠DCA and ∠BAC subtend arcs AD and BC respectively in the circle. Therefore, we can say:
∠DCA=∠BAC⟹Arc AD=Arc BC
(Angles subtended by the same arc are equal).
5. Apply the Circle Theorem:
Since the arcs AD and BC are equal, we can use the theorem that states equal arcs in a circle subtend equal chords. Thus:
AD=BC
6. Conclusion:
We have proved that in the cyclic trapezium ABCD, the sides AD and BC are equal.
Final Statement:
Therefore, we conclude that AD=BC.
---
We are given a cyclic trapezium ABCD where AB is parallel to DC.
Draw trapezium ABCD with AB parallel to DC. Label the points accordingly.
Since AB∥DC, we can use the property of alternate interior angles. When we draw a transversal line AC, we have:
∠DCA=∠BAC
(Alternate interior angles are equal).
The angles ∠DCA and ∠BAC subtend arcs AD and BC respectively in the circle. Therefore, we can say:
∠DCA=∠BAC⟹Arc AD=Arc BC
(Angles subtended by the same arc are equal).
Since the arcs AD and BC are equal, we can use the theorem that states equal arcs in a circle subtend equal chords. Thus:
AD=BC
We have proved that in the cyclic trapezium ABCD, the sides AD and BC are equal.
Therefore, we conclude that AD=BC.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
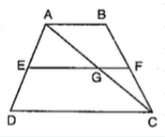
View Solution
Knowledge Check
In a trapezium ABCD, AB is parallel to CD. If E is midpoint of side AD and a line drawn from point E, parallel to the parallel sides cuts BC at F then
ABF = CF if AD = BCBBF = CF ia always trueCBF:CF is less than 1 if AD<BCDBF:CF is greater than 1 if AD>BCABCD is a cyclic trapezium whose side AD and BC are parallel to each other. If ∠ABC=62∘ then the measure of the ∠BCD is :
A120∘B118∘C62∘D28∘ABCD is a cyclic trapezium whose sides AD and BC are parallel to each other. If ∠ABC=72∘, then the measure of the ∠BCD is
A162∘B18∘C108∘D72∘
In rectangle ABCD, E is the midpoint of side BC. Prove that, AE = DE.
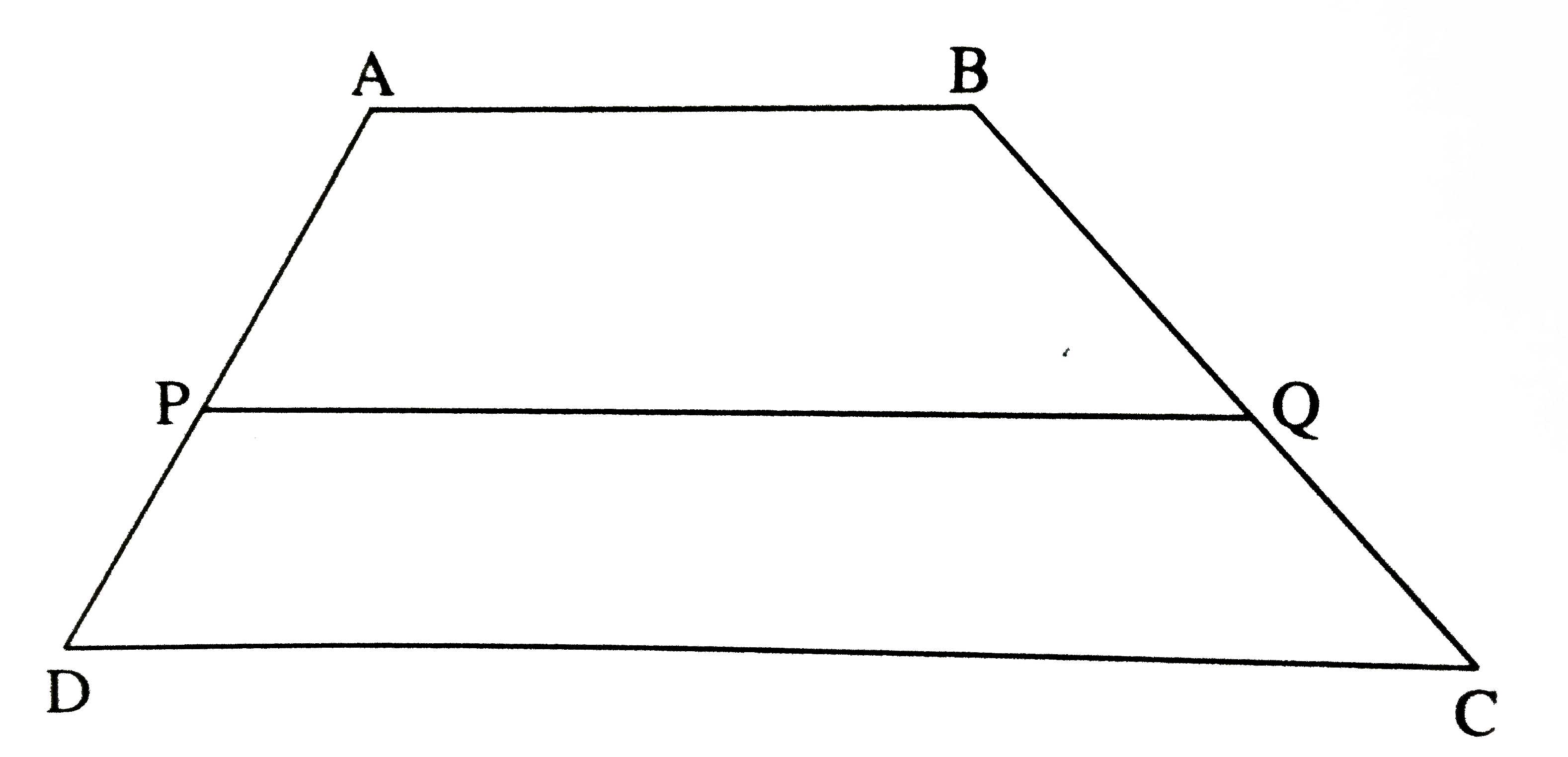
View SolutionIn trapezium ABCD side AB∣∣ side PQ∣∣ side DC,AP=15,PD=12,QC=14, find BQ.
View SolutionThe line segments joining the midpoints M and N of parallel sides AB and DC respectively of a trapezium ABCD is perpendicular to both the sides AB and DC. Prove that AD=BC
View SolutionIn quadrilateral ABCD, side AB is parallel to side DC.IF∠A:∠D=1:2and∠C:∠B=4:5.
(i) Calculate wach angle of the quadrilateral.
(ii) Assign special name to quadrilateral ABCD.
View SolutionIn ΔABC,D is any point on side BC. Prove that
AB+BC+CA>2AD
View Solution
