In a ΔABC, if median AD is perpendicular to AB, the tanA+2tanB is equal to
1
3
0
12
To solve the problem, we need to find the value of tanA+2tanB in triangle ABC given that the median AD is perpendicular to AB.
1. Understand the Geometry:
- In triangle ABC, AD is the median from vertex A to side BC. Since AD is a median, it divides BC into two equal segments, BD and DC.
- Given that AD is perpendicular to AB, we have ∠ADB=90∘.
2. Label Angles:
- Let ∠A=A, ∠B=B, and ∠C=C.
- Since AD is perpendicular to AB, we can denote ∠ADB=90∘ and ∠DAB=A.
3. Using the Exterior Angle Theorem:
- According to the exterior angle theorem, the exterior angle ∠ADC is equal to the sum of the opposite interior angles:
∠ADC=∠A+∠B
- Since AD is perpendicular to AB, we can express ∠BDC as:
∠BDC=90∘−B
4. Relate Angles Using Trigonometric Identities:
- In triangle ABD, we can use the tangent function:
tanA=BDADandtanB=ADBD
- Since AD is the median and BD=DC, we can express BD in terms of AD.
5. Using the Cotangent Function:
- We know that cot(90∘+B)=−tanB. Therefore, we can write:
tanA+2tanB=0
- This implies:
tanA=−2tanB
6. Conclusion:
- Thus, we have shown that:
tanA+2tanB=0
Final Result:
tanA+2tanB=0
- In triangle ABC, AD is the median from vertex A to side BC. Since AD is a median, it divides BC into two equal segments, BD and DC.
- Given that AD is perpendicular to AB, we have ∠ADB=90∘.
- Let ∠A=A, ∠B=B, and ∠C=C.
- Since AD is perpendicular to AB, we can denote ∠ADB=90∘ and ∠DAB=A.
- According to the exterior angle theorem, the exterior angle ∠ADC is equal to the sum of the opposite interior angles:
∠ADC=∠A+∠B
- Since AD is perpendicular to AB, we can express ∠BDC as:
∠BDC=90∘−B
- In triangle ABD, we can use the tangent function:
tanA=BDADandtanB=ADBD
- Since AD is the median and BD=DC, we can express BD in terms of AD.
- We know that cot(90∘+B)=−tanB. Therefore, we can write:
tanA+2tanB=0
- This implies:
tanA=−2tanB
- Thus, we have shown that:
tanA+2tanB=0
tanA+2tanB=0
Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 3
34 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 4
10 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
tan3A−tan2A−tanA= is equal to
View SolutionIn a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
View SolutionIf the median of a triangle through A is perpendicular to AB, then
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that :
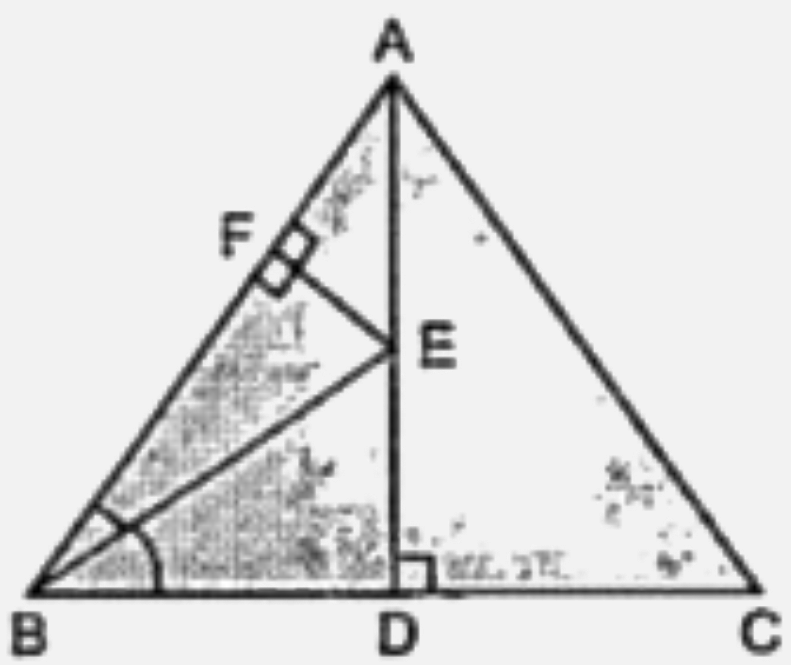
ED=EF
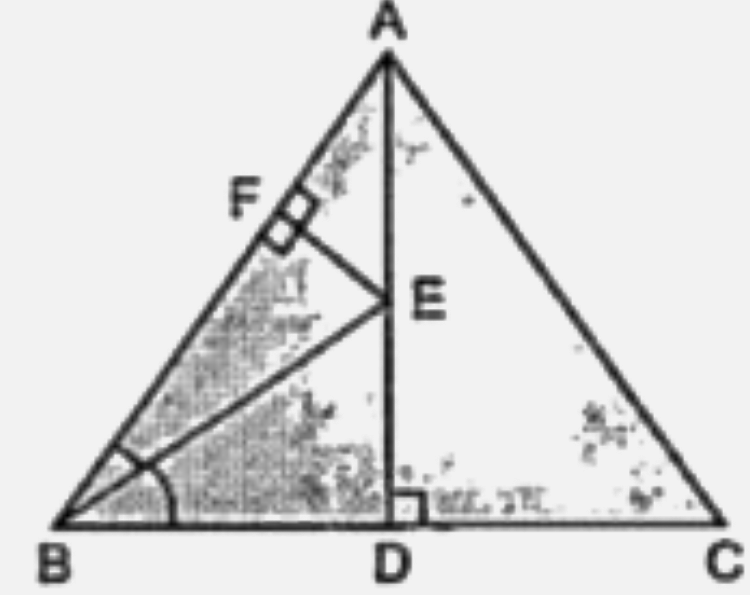
View SolutionIn the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED=EF
View SolutionIf the median of triangle ABC through A is perpendicular AB, then the value of sinA cosB + 2sinB cosA is equal to
View SolutionIn Triangle ABC, AD is perpendicular to BC, tanB=34tanC=512 and BC = 56 cm . Calculate the lengths of AD.
View SolutionIn any ΔABC the value of 1−tanB2tanC2 is equal to :-
View SolutionIf A(4,−6),B(3,−2)andC(5,2) are the vertices of a ΔABCandAD is its median, prove that the median AD divides ΔABC into two triangles of equal areas.
View SolutionIf in a triangle ABC, b + c = 3a, then tan(B2)tan(C2) is equal to
View Solution
