In Triangle ABC, AD is perpendicular to BC, tanB=34tanC=512 and BC = 56 cm . Calculate the lengths of AD.
The correct Answer is:15cm
To solve the problem, we need to find the length of AD in triangle ABC, where AD is perpendicular to BC. We are given the following information:
- tanB=34
- tanC=512
- BC=56cm
Let's denote:
- BD=x
- DC=y
- AD=h
Since BC=BD+DC, we have:
x+y=56(1)
Step 1: Express h in terms of x using tanB
From triangle ADB, we can express tanB:
tanB=ADBD=hx
Given tanB=34, we can write:
hx=34
Cross-multiplying gives:
4h=3x(2)
Step 2: Express h in terms of y using tanC
From triangle ADC, we can express tanC:
tanC=ADDC=hy
Given tanC=512, we can write:
hy=512
Cross-multiplying gives:
12h=5y(3)
Step 3: Solve equations (2) and (3)
From equation (2):
h=34x
From equation (3):
h=512y
Now we can set these two expressions for h equal to each other:
34x=512y
Step 4: Express y in terms of x
Cross-multiplying gives:
3⋅12x=4⋅5y
36x=20y
y=3620x=95x(4)
Step 5: Substitute equation (4) into equation (1)
Substituting y in equation (1):
x+95x=56
Combining terms:
55x+95x=56
145x=56
Step 6: Solve for x
Multiplying both sides by 514:
x=56⋅514=20
Step 7: Find y
Using equation (4) to find y:
y=95x=95⋅20=36
Step 8: Find h using x
Now we can find h using equation (2):
h=34x=34⋅20=15
Conclusion
The length of AD is:
15cm
---
- tanC=512
- BC=56cm
- BD=x
- DC=y
- AD=h
x+y=56(1)
From triangle ADB, we can express tanB:
tanB=ADBD=hx
Given tanB=34, we can write:
hx=34
Cross-multiplying gives:
4h=3x(2)
From triangle ADC, we can express tanC:
tanC=ADDC=hy
Given tanC=512, we can write:
hy=512
Cross-multiplying gives:
12h=5y(3)
From equation (2):
h=34x
h=512y
34x=512y
Cross-multiplying gives:
3⋅12x=4⋅5y
36x=20y
y=3620x=95x(4)
Substituting y in equation (1):
x+95x=56
Combining terms:
55x+95x=56
145x=56
Multiplying both sides by 514:
x=56⋅514=20
Using equation (4) to find y:
y=95x=95⋅20=36
Now we can find h using equation (2):
h=34x=34⋅20=15
The length of AD is:
15cm
Topper's Solved these Questions
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:CO-ORDINATE GEOMETRY
Explore 6 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:GRAPHICAL SOLUTION
Explore 3 Videos
- CHAPTERWISE REVISION (STAGE 3) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 3) Exercise:SOLIDS
Explore 6 Videos
- CHAPTERWISE REVISION (STAGE 1) Book:ICSEChapter:CHAPTERWISE REVISION (STAGE 1) Exercise:Graphical solution
Explore 10 Videos
- CIRCLEBook:ICSEChapter:CIRCLEExercise:EXERCISE 17(D)
Explore 12 Videos
Similar Questions
In a triangle ABC , AP is perpendicular to BC . If BC = 112 cm , cot B =43 and cot C =125 , calculate the length of AP
View SolutionIn triangles ABC , AD is perpendicular to BC and AD2=BD×DC . Prove that angle BAC=90∘
View SolutionIn triangle ABC,AD is perpendicular to side BC and AD2=BD×DC.
Show that angle BAC=90∘.
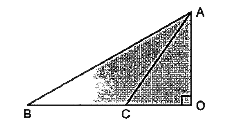
View SolutionIn triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC
View SolutionIn triangle ABC, AD is perpendicular to BC. sin B = 0.8, BD = 9 cm and tan C = 1. Find the length of AB, AD, AC and DC.
View SolutionIn a ΔABC, the median AD is perpendicular to AC. If b = 5 and c = 11, then a =
View SolutionIn the ΔABC the foot of the perpendicular from A to BC is D. Given that tanB=43,cosC=1517and that AB=20cm, calculate without using tables
(i) the lengths of the sides AC and BC,
(ii) the value of sin A.
View SolutionΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
View SolutionABC is an isosceles triangle with AB = AC =13 cm and BC = 10 cm. Calculate the length of the perpendicular from A to BC.
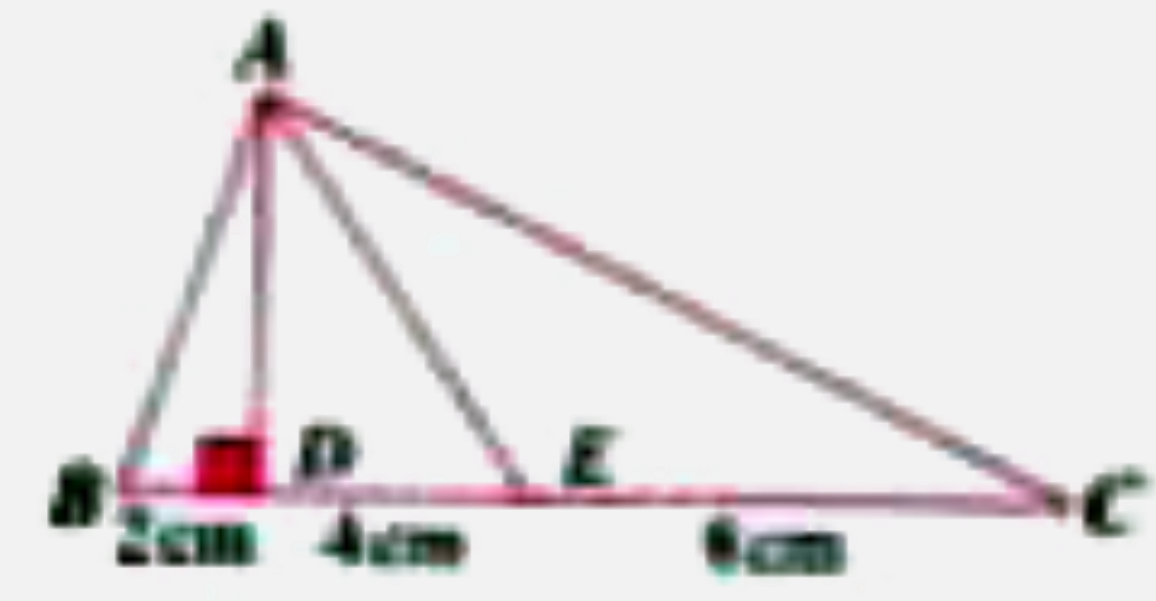
View SolutionA triangle ABC is such that AD is perpendicular to BC and E is a point on DC. Also. Given that BD=2cm,DE=4cm,andEC=8cm. Find the ratio of the areas of ΔABC , ΔADEandΔAEC.
View Solution