In a ΔABC, right-angled at B, if AB=x2,BC=x+2andAC=x+3, then the quadratic equation, formed in x, is :
x2−8x−20=0
x2−2x+5=0
x2+8x+20=0
x2+2x+5=0
The correct Answer is:A
To solve the problem, we will use the Pythagorean theorem, which states that in a right-angled triangle, the square of the hypotenuse (AC) is equal to the sum of the squares of the other two sides (AB and BC).
1. Identify the sides of the triangle:
- Given:
- AB=x2
- BC=x+2
- AC=x+3
2. Apply the Pythagorean theorem:
- According to the theorem:
AC2=AB2+BC2
- Substitute the values:
(x+3)2=(x2)2+(x+2)2
3. Expand both sides:
- Left side:
(x+3)2=x2+6x+9
- Right side:
(x2)2=x24
(x+2)2=x2+4x+4
- Combine the right side:
x24+x2+4x+4=x24+4x24+4x+4=5x24+4x+4
4. Set the equation:
- Now we have:
x2+6x+9=5x24+4x+4
5. Eliminate the fraction:
- Multiply the entire equation by 4 to eliminate the fraction:
4(x2+6x+9)=5x2+16x+16
- This simplifies to:
4x2+24x+36=5x2+16x+16
6. Rearrange the equation:
- Move all terms to one side:
4x2+24x+36−5x2−16x−16=0
- Combine like terms:
−x2+8x+20=0
- Multiply through by -1 to make the leading coefficient positive:
x2−8x−20=0
7. Final quadratic equation:
- The quadratic equation formed in x is:
x2−8x−20=0
- Given:
- AB=x2
- BC=x+2
- AC=x+3
- According to the theorem:
AC2=AB2+BC2
- Substitute the values:
(x+3)2=(x2)2+(x+2)2
- Left side:
(x+3)2=x2+6x+9
- Right side:
(x2)2=x24
(x+2)2=x2+4x+4
- Combine the right side:
x24+x2+4x+4=x24+4x24+4x+4=5x24+4x+4
- Now we have:
x2+6x+9=5x24+4x+4
- Multiply the entire equation by 4 to eliminate the fraction:
4(x2+6x+9)=5x2+16x+16
- This simplifies to:
4x2+24x+36=5x2+16x+16
- Move all terms to one side:
4x2+24x+36−5x2−16x−16=0
- Combine like terms:
−x2+8x+20=0
- Multiply through by -1 to make the leading coefficient positive:
x2−8x−20=0
- The quadratic equation formed in x is:
x2−8x−20=0
Similar Questions
Knowledge Check
ΔABC is right angled at A. if AB = 24 mm and AC = 7 mm, then BC is
A20 mmB25 mmC30 mmD35 mmIn a right-angled triangle ABC, right angled at B, AB=x2, BC = x + 2 and AC = x + 3. The value of x is :
A5B10C12D14In ΔABC,AB=a−b,AC=√a2+b2 and BC=√2ab, then find angle B.
A60∘B30∘C90∘D45∘
In ΔABC, right angled at B, AB = 5 cm and ∠ACB==30∘. Find BC and AC.
View SolutionIn △ABC, right angled at B, if AB:BC=3:4 and AC=20, then find AB and BC.
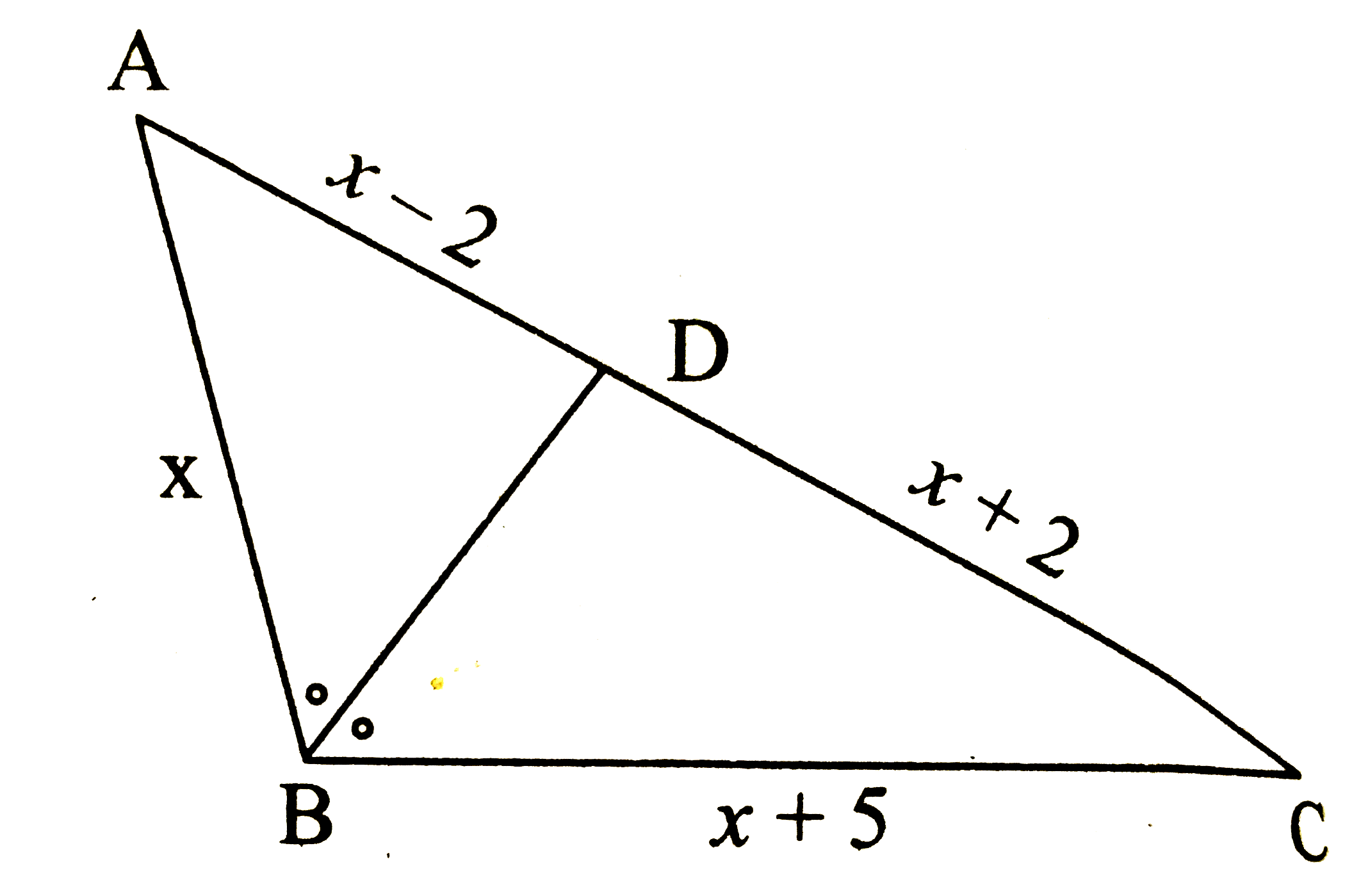
View SolutionIn ΔABC set BD bisects ∠ABC. If AB−x,BC=x+5,AD=x−2,DC=x+2, then find the value of x.

View SolutionIn ΔABC, seg BD bisects ∠ABC. If AB=x, BC=x+5, AD=x−2, DC=x+2. Find the value of x.
View SolutionIn ΔABC D and E are points on sides AB and AC, such that DE || BC. If AD = x,DB = x - 2, AE = x + 2 and EC = x-1 then the value of x is
View Solution
