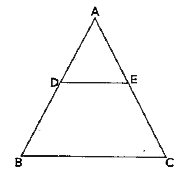
In ΔABC D and E are points on sides AB and AC, such that DE || BC. If AD = x,DB = x - 2, AE = x + 2 and EC = x-1 then the value of x is
4
2
1
8
The correct Answer is:A
To solve the problem, we will use the properties of similar triangles. Given that DE∥BC, we can establish a proportion between the segments of the sides of triangle ABC and triangle ADE.
1. Identify the segments:
- Let AD=x
- Let DB=x−2
- Let AE=x+2
- Let EC=x−1
2. Calculate the lengths of sides AB and AC:
- The length of side AB is:
AB=AD+DB=x+(x−2)=2x−2
- The length of side AC is:
AC=AE+EC=(x+2)+(x−1)=2x+1
3. Set up the proportion using the similarity of triangles:
Since DE∥BC, the triangles ADE and ABC are similar. Therefore, we can write:
ADAB=AEAC
Substituting the lengths we found:
x2x−2=x+22x+1
4. Cross-multiply to eliminate the fractions:
x(2x+1)=(x+2)(2x−2)
5. Expand both sides:
- Left side:
2x2+x
- Right side:
(x+2)(2x−2)=2x2−2x+4x−4=2x2+2x−4
6. Set the equation:
2x2+x=2x2+2x−4
7. Simplify the equation:
Subtract 2x2 from both sides:
x=2x−4
Rearranging gives:
x−2x=−4⟹−x=−4⟹x=4
8. Conclusion:
The value of x is 4.
- Let AD=x
- Let DB=x−2
- Let AE=x+2
- Let EC=x−1
- The length of side AB is:
AB=AD+DB=x+(x−2)=2x−2
- The length of side AC is:
AC=AE+EC=(x+2)+(x−1)=2x+1
Since DE∥BC, the triangles ADE and ABC are similar. Therefore, we can write:
ADAB=AEAC
Substituting the lengths we found:
x2x−2=x+22x+1
x(2x+1)=(x+2)(2x−2)
- Left side:
2x2+x
- Right side:
(x+2)(2x−2)=2x2−2x+4x−4=2x2+2x−4
2x2+x=2x2+2x−4
Subtract 2x2 from both sides:
x=2x−4
Rearranging gives:
x−2x=−4⟹−x=−4⟹x=4
The value of x is 4.
Topper's Solved these Questions
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.1
45 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - INTRODUCTORY EXERCISE - 12.2
100 Videos
- GEOMETRYBOOK - ARIHANT SSCCHAPTER - GEOMETRYEXERCISE - EXERCISE(LEVEL 2)
52 Videos
- FUNDAMENTALS BOOK - ARIHANT SSCCHAPTER - FUNDAMENTALS EXERCISE - TEST OF YOU - LEARNING - 2
40 Videos
- HCF AND LCMBOOK - ARIHANT SSCCHAPTER - HCF AND LCMEXERCISE - Exercise Higher Skill Level Questions
18 Videos
Similar Questions
Knowledge Check
A sum of money lent at compound interest for 2 years at 20% per annum would fetch Rs 482 more, if the interest was payable half-yearly than if it was payable annually. The sum is: (a) Rs 10,000 (b) Rs 20,000 (c) Rs 40,000 (d) Rs 50,000
AA. 30000BB. 20000CC. 10000DD.50000In ΔABC, DE || BC. If AD = 2x - 1, AE = 2x + 5, BD = x - 3 and CE = x - 1, then the value of x is:
A8B9C10D11In ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cm
In Figure, DEBC, if AD=x,DB=x−2,AE=x+2 and EC=x−1, find the value of x.
View SolutionIn ΔABC,D and E are points on the sides AB and AC respectively ,such that DE||BC. If AD=2.5cm,BD=3cm and AE =3.75 cm , then the value of AC.
View SolutionIn ΔABC, D and E are points on sides AB and AC respectively such that DE∣∣BC. If AE=1.8cm, BD= 7.2cm and CE= 5.4cm, then the length of AD is
View SolutionIn △ABC, D and E are points on the sides AB and AC, respectively, such that DE || BC. If AD = 5cm, DB = 9cm AE =4cm and BC = 15.4cm, then the sum of the length of DE and EC (in cm) is:
△ABC में, D और E क्रमशः AB और AC भुजाओं पर बिंदु इस प्रकार है की DE||BC, यदि AD = 5cm, DB = 9cm AE = 4cm और BC = 15.4cm है, तो DE और EC (सेमी में) की लंबाई का योग है
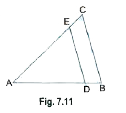
View SolutionIn Fig. 7.11, De||BC. If AD= x, DB= x- 2, AE = x + 2 and EC =x -1, find the value of x.
View Solution