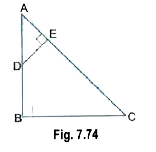
In a ΔABC,BD⊥CA and CE⊥BA, Prove that ΔABD~ΔACE.
To prove that triangle ΔABD is similar to triangle ΔACE, we will use the Angle-Angle (AA) similarity criterion.
1. Identify the Given Information:
- We have triangle ABC.
- BD is perpendicular to CA, which means ∠ADB=90∘.
- CE is perpendicular to BA, which means ∠AEC=90∘.
2. Draw the Triangles:
- Draw triangle ABC with points A,B,C.
- Mark point D on line CA such that BD is perpendicular to CA.
- Mark point E on line BA such that CE is perpendicular to BA.
3. Identify Common Angles:
- Both triangles ABD and ACE share the angle ∠A.
4. Establish Right Angles:
- From the perpendicular lines, we have:
- ∠ADB=90∘ (from BD⊥CA)
- ∠AEC=90∘ (from CE⊥BA)
5. Apply the Angle-Angle Criterion:
- We have:
- ∠ADB=90∘
- ∠AEC=90∘
- ∠A is common to both triangles.
- Therefore, we can state:
- ∠ADB=∠AEC
- ∠A is common.
- By the Angle-Angle (AA) similarity criterion, since two angles of triangle ABD are equal to two angles of triangle ACE, we conclude that:
ΔABD∼ΔACE
Conclusion:
Thus, we have proved that triangle ΔABD is similar to triangle ΔACE using the Angle-Angle similarity criterion.
- We have triangle ABC.
- BD is perpendicular to CA, which means ∠ADB=90∘.
- CE is perpendicular to BA, which means ∠AEC=90∘.
- Draw triangle ABC with points A,B,C.
- Mark point D on line CA such that BD is perpendicular to CA.
- Mark point E on line BA such that CE is perpendicular to BA.
- Both triangles ABD and ACE share the angle ∠A.
- From the perpendicular lines, we have:
- ∠ADB=90∘ (from BD⊥CA)
- ∠AEC=90∘ (from CE⊥BA)
- We have:
- ∠ADB=90∘
- ∠AEC=90∘
- ∠A is common to both triangles.
- Therefore, we can state:
- ∠ADB=∠AEC
- ∠A is common.
- By the Angle-Angle (AA) similarity criterion, since two angles of triangle ABD are equal to two angles of triangle ACE, we conclude that:
ΔABD∼ΔACE
Thus, we have proved that triangle ΔABD is similar to triangle ΔACE using the Angle-Angle similarity criterion.
Topper's Solved these Questions
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART A (SECTION-II)
8 Videos
- SAMPLE PAPER 13BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 13EXERCISE - PART B (SECTION-III)
8 Videos
- SAMPLE PAPER 11 (SELF - ASSESSMENT)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 11 (SELF - ASSESSMENT)EXERCISE - SECTION -C
10 Videos
- SAMPLE PAPER 2 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 2 EXERCISE - SECTION - D
9 Videos
Similar Questions
Knowledge Check
In a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤AD
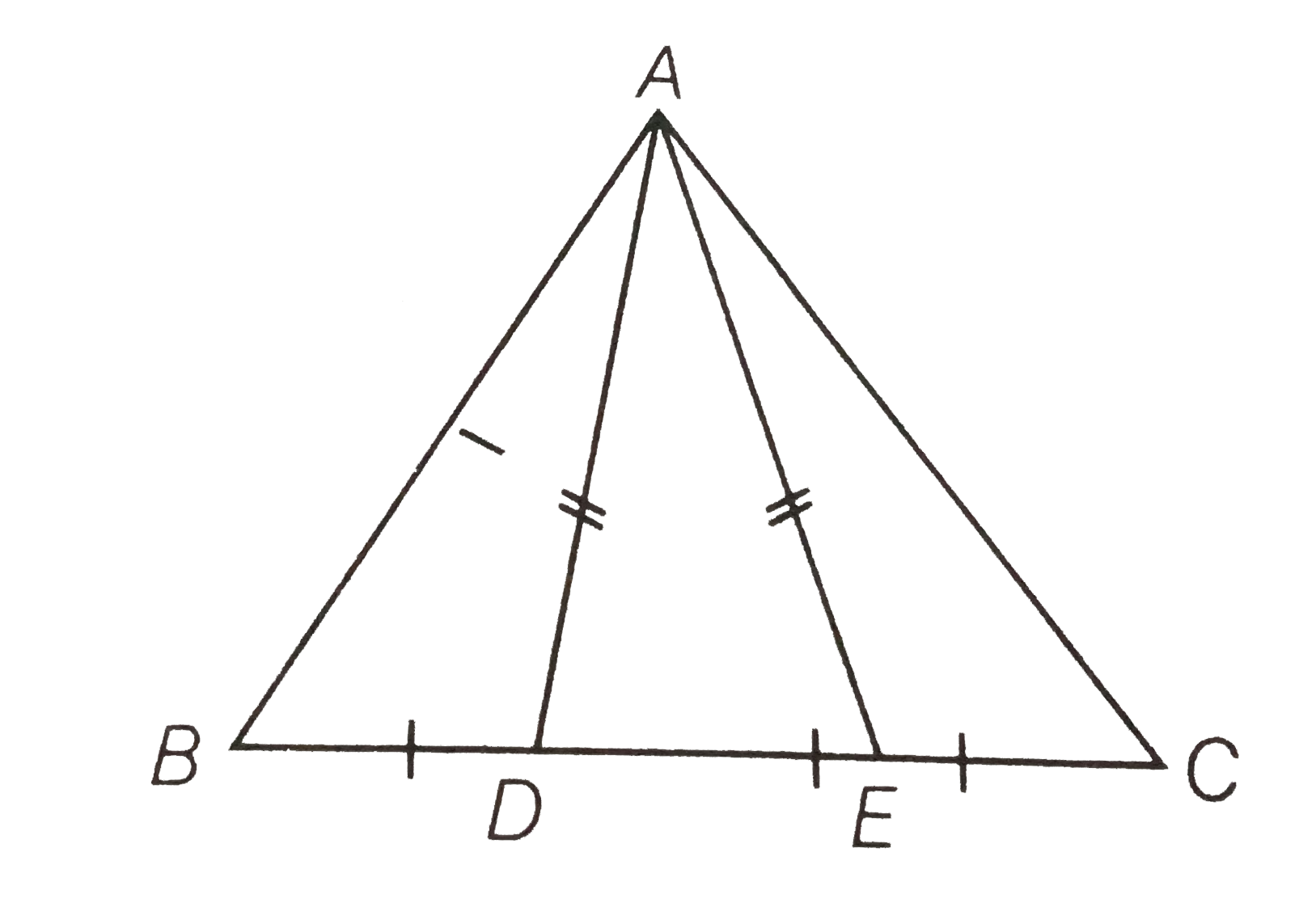
In the given figure, D and E are points on the side BC of a ΔABC such that BD = CE and AD = AE. Show that ΔABD≅ΔACE.
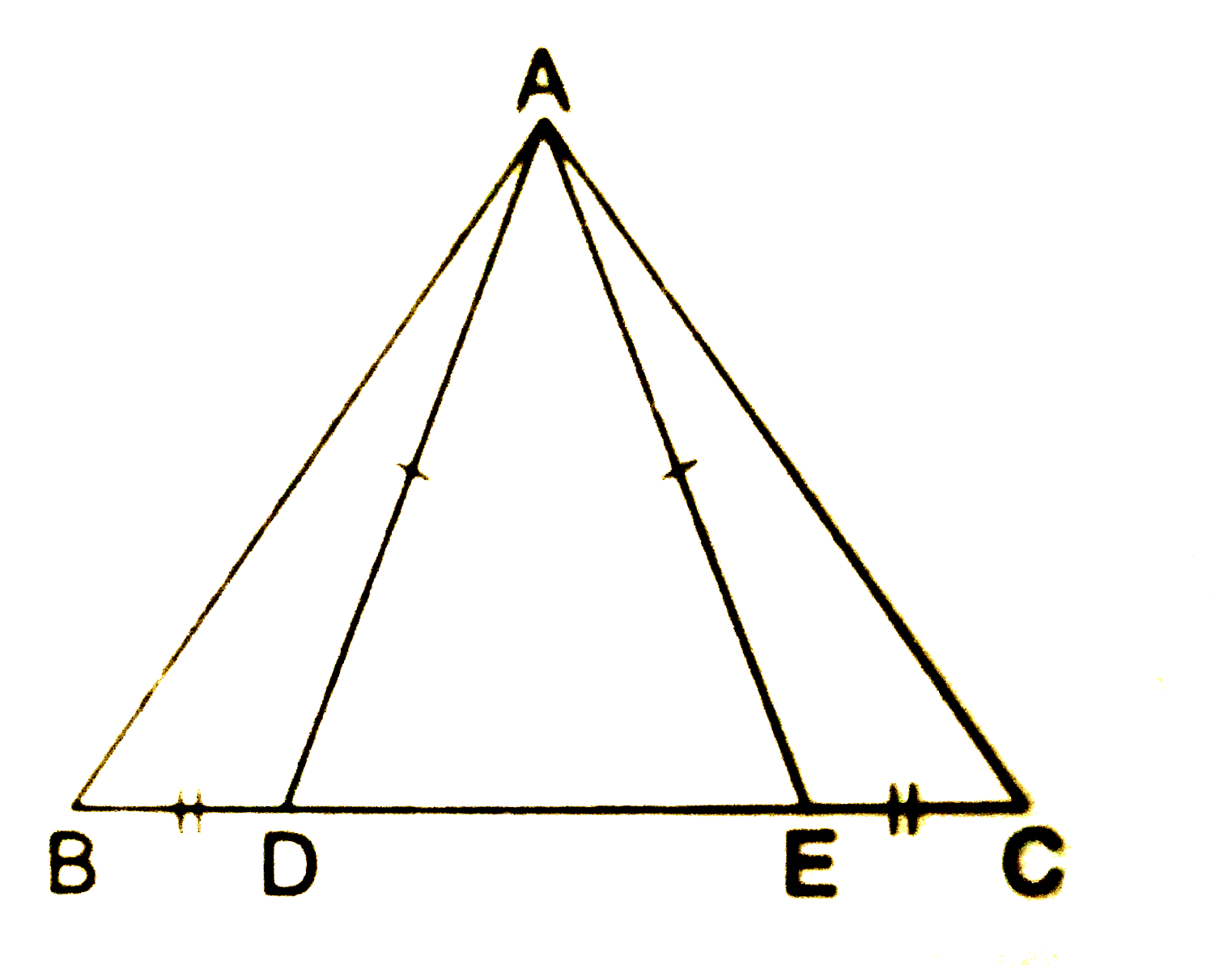
View SolutionIn figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE.Show that ΔABD≅ΔACE.
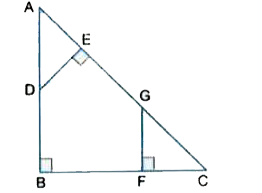
View SolutionIn the given fig; AB⊥BC,FG⊥BC, and DE⊥AC. Prove that △ADE~△GCF.
View SolutionIn a ΔABC, ∠B is an acute-angle and AD⊥BC. Prove that:
AB2+CD2=AC2+BD2
View SolutionFig. 5.96,AB=EF,BC=DE,AB⊥BDandFE⊥CE. Prove that ΔABD≡ΔFEC.
View SolutionIn the adjoining figure, BD = CE and ∠ADB=∠AEC=90∘, prove that
(i) ΔABD≅ΔACE (ii) ABC is an isosceles triangle.

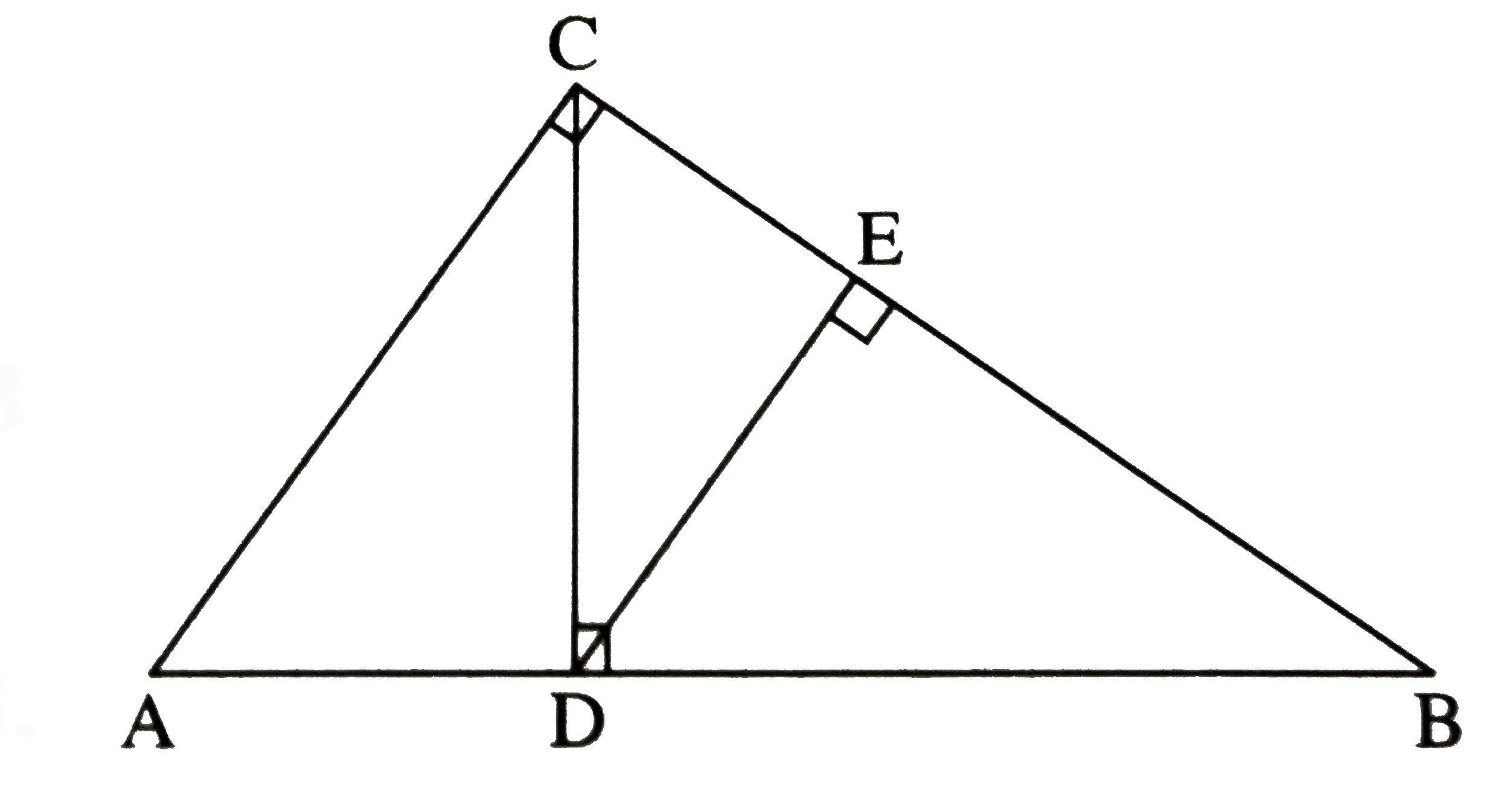
View SolutionIn △ ABC ,
∠ACB=90∘ ,
CD⊥AB and
DE⊥CB
Prove that CD2×AC=AD×AB×DE .
View Solution