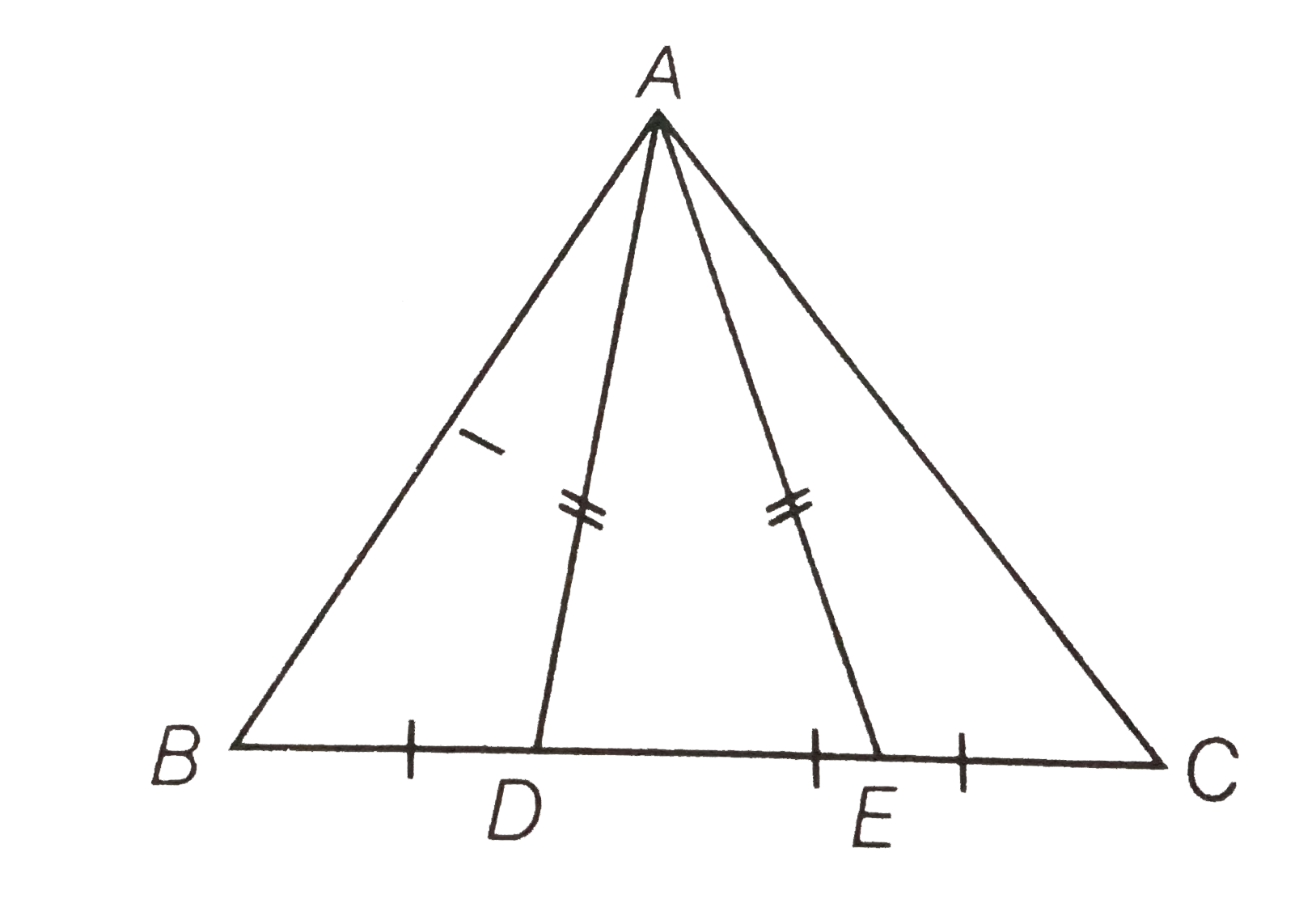
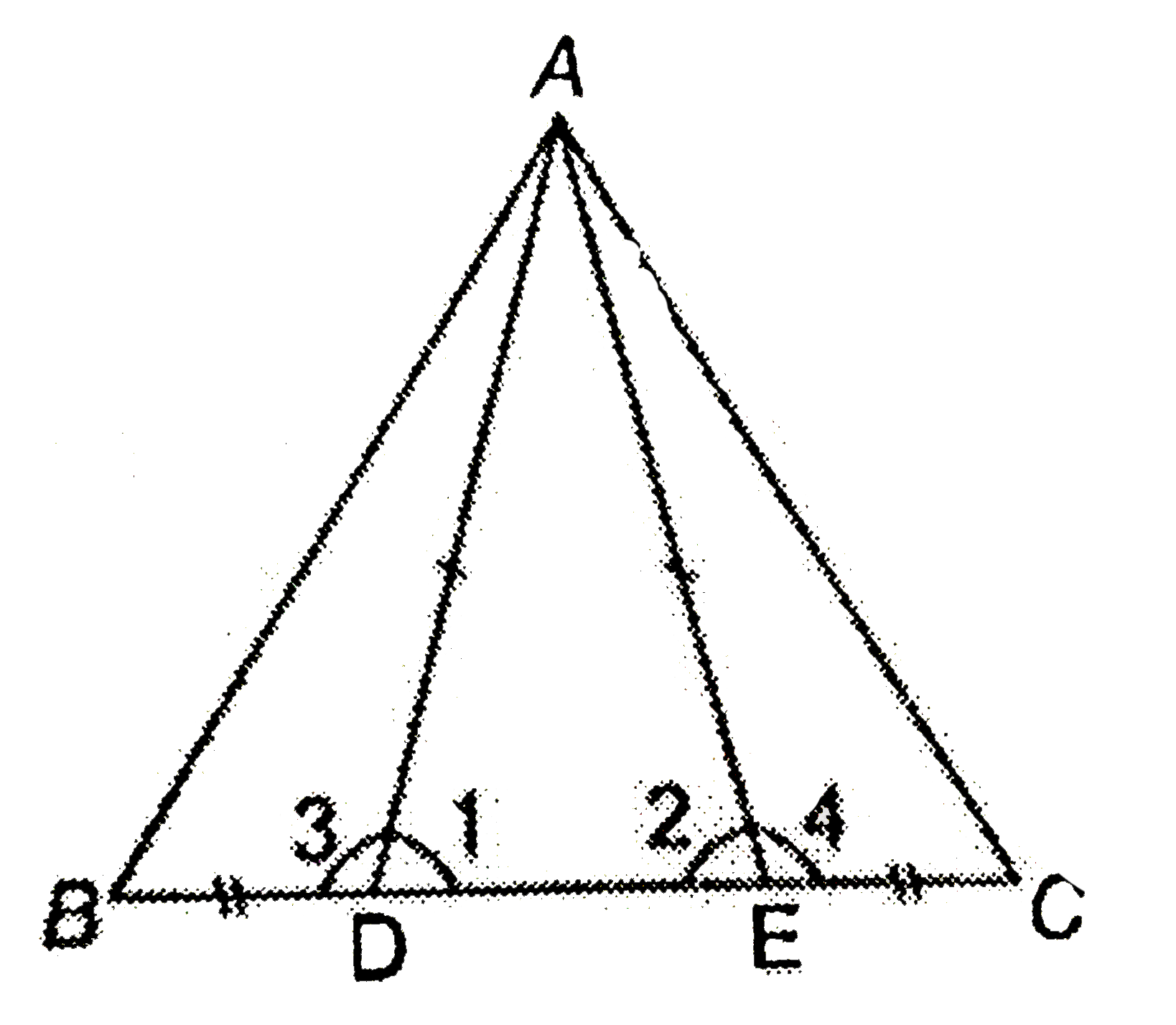
In the given figure, D and E are points on the side BC of a ΔABC such that BD = CE and AD = AE. Show that ΔABD≅ΔACE.
GIVEN A ΔABC in which DandE are points on BC such that BD = CE and AD = AE.
TO PROVE ΔABD≅ΔACE.
PROOF We know that the angles opposite to equal sides of a triangle are equal.
So, in ΔADE, we have
AD=AE⇒∠ADE=∠AED
⇒ 180∘−∠ADE=180∘−∠AED
⇒ ∠ADB=∠AEC. ...(i)
Now, in ΔABDandΔACE, we have
AD=AE (given)
∠ADB=∠AEC [proved in (i)]
BD=CE (given)
∴ ΔABD≅ΔACE. (SAS-criteria).
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A27videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B16videos
CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLE
- BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)37videos
CIRCLES
- BOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)22videos
COORDINATE GEOMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
D is a point on the side BC of a ΔABC such that AD bisects ∠BAC . Then
ABD=CDBBA>BDCBD>BADCD>CA
A point D is taken on the side BC of a ΔABC such that BD=2DC. Prove that ar(ΔABD)=2ar(ΔADC)
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
 View Solution
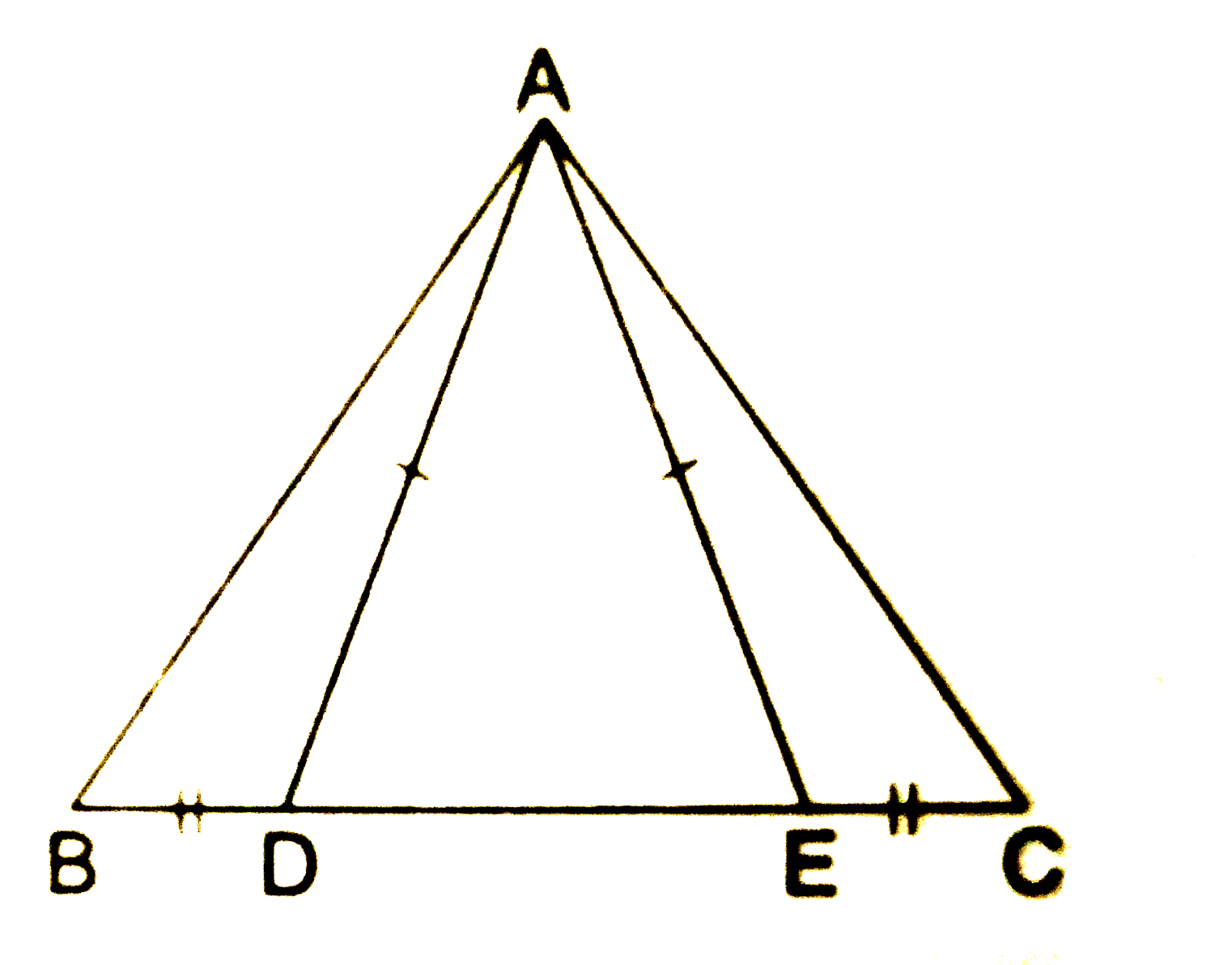
View SolutionIn the given figure, AB = AC and AD = AE. Prove that:
ΔABD≅ΔACE
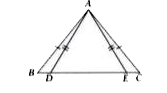 View Solution
View Solutionif D and E are points on the sides AB and AC of a ΔABC. Such that AB=12 cm, AD=8 cm, AE=12 cm, AC= 18 cm. show that DE||BC.
View SolutionIn a ΔABC,BD⊥CA and CE⊥BA, Prove that ΔABD~ΔACE.
View SolutionD is a point on side BC of triangle ABC such that AD = AC (see figure). Show that AB>AD.
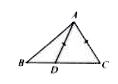 View Solution
View SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
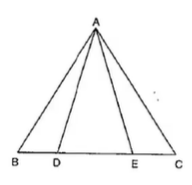 View Solution
View Solution