In a group of 40 students , 23 take the AP Psycholgy class , 18 take the AP Calculas
class, and 8 take both classes . What is the probability that a student takes AP
Psychology or AP Calculus ?
To solve the problem step by step, we will use the principle of probability for the union of two events.
Step 1: Define the Events
Let:
- Event A = the event that a student takes AP Psychology.
- Event B = the event that a student takes AP Calculus.
Step 2: Identify the Given Values
From the problem, we have:
- Total number of students = 40
- Number of students taking AP Psychology (|A|) = 23
- Number of students taking AP Calculus (|B|) = 18
- Number of students taking both classes (|A ∩ B|) = 8
Step 3: Calculate the Probability of Each Event
We can calculate the probabilities of each event:
- Probability of A (P(A)) = Number of students taking AP Psychology / Total number of students
P(A)=2340
- Probability of B (P(B)) = Number of students taking AP Calculus / Total number of students
P(B)=1840
- Probability of A and B (P(A ∩ B)) = Number of students taking both classes / Total number of students
P(A∩B)=840
Step 4: Use the Formula for the Union of Two Events
To find the probability that a student takes either AP Psychology or AP Calculus, we will use the formula for the union of two events:
P(A∪B)=P(A)+P(B)−P(A∩B)
Step 5: Substitute the Values into the Formula
Now we substitute the values we calculated:
P(A∪B)=2340+1840−840
Step 6: Perform the Calculation
Combine the fractions:
P(A∪B)=23+18−840=3340
Final Answer
The probability that a student takes AP Psychology or AP Calculus is:
3340
---
Let:
- Event A = the event that a student takes AP Psychology.
- Event B = the event that a student takes AP Calculus.
From the problem, we have:
- Total number of students = 40
- Number of students taking AP Psychology (|A|) = 23
- Number of students taking AP Calculus (|B|) = 18
- Number of students taking both classes (|A ∩ B|) = 8
We can calculate the probabilities of each event:
- Probability of A (P(A)) = Number of students taking AP Psychology / Total number of students
P(A)=2340
P(B)=1840
P(A∩B)=840
To find the probability that a student takes either AP Psychology or AP Calculus, we will use the formula for the union of two events:
P(A∪B)=P(A)+P(B)−P(A∩B)
Now we substitute the values we calculated:
P(A∪B)=2340+1840−840
Combine the fractions:
P(A∪B)=23+18−840=3340
The probability that a student takes AP Psychology or AP Calculus is:
3340
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - PROBABILITY EXERCISE - EXERCISES16videos
PROBABILITY
- BOOK - ENGLISH SATCHAPTER - PRACTICE TEST 5 - MATHEMATICS TESTEXERCISE - EXERCISE60videos
PRACTICE TEST 5 - MATHEMATICS TEST
- BOOK - ENGLISH SATCHAPTER - PROBLEM SOLVING AND DATA ANALYSISEXERCISE - EXERICSE80videos
PROBLEM SOLVING AND DATA ANALYSIS
Similar Questions
In a school there are 1000 students , out of which 430 girls . It is known that out of 430 , 10% of the girls study in class XII. What is the probability that a students chosen randomly studies in class XII ,given that the chosen students is a girl
View SolutionIn a school there are 1000 students, out of which 430 are girls. It is known that out of 430, 10% of the girls study in class XII. What is the probability that a student chosen randomly studies in class XII given that the chosen student is a girl?
View Solution
Knowledge Check
- Question 1 - Select One
In a group of 30 students, 20 take French, 15 take Spanish, and 5 take neither language. How many students take both French and Spanish?
A0B5C10D15 - Question 2 - Select One
The graph below shows the number of students who were present on Thursday from each of the 5 groups in Ms. Meagan's class. What is the probability that a student selected at random from the class on Thrusday is in Group 4?
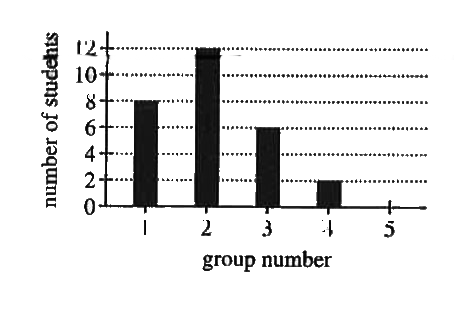 A128B114C15D14
A128B114C15D14 - Question 3 - Select One
A class has 12 boys and 4 girls. If three students are selected at random from the class,
what is the probability that all will be boys?A155B14C13D1128
In a school there are 1000 students, out of which 430 are girls. It is known that out of 430, 10% of the girls study in class XII. What is the probability that a student chosen randomly studies in Class XII given that the chosen student is a girl
View SolutionOut of 32 students,8 are absent from the class. What is the percentage of the students who are absent?
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passed in only one subject.
View SolutionIn a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passes in only one subject.
View SolutionIn a particular section of class IX, 40 students were asked about the month of their birth and the following graph was prepared for the data so obtained.

Find the probability that a student of the class was born in August.View Solution

