In a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passes in only one subject.
The correct Answer is:13/25
To solve the problem step by step, we will use the principle of inclusion-exclusion to find the number of students who passed in only one subject (Mathematics or Statistics).
1. Define the Events:
- Let A be the event that a student passed in Mathematics.
- Let B be the event that a student passed in Statistics.
2. Given Data:
- Total number of students, n=125
- Number of students who passed in Mathematics, |A|=70
- Number of students who passed in Statistics, |B|=55
- Number of students who passed in both subjects, |A∩B|=30
3. Calculate Students Passing Only Mathematics:
- Students who passed only Mathematics can be calculated as:
|A only|=|A|−|A∩B|=70−30=40
4. Calculate Students Passing Only Statistics:
- Students who passed only Statistics can be calculated as:
|B only|=|B|−|A∩B|=55−30=25
5. Total Students Passing Only One Subject:
- The total number of students passing only one subject is:
|A only|+|B only|=40+25=65
6. Calculate the Probability:
- The probability that a student selected at random passes in only one subject is given by:
P(only one subject)=|A only|+|B only|n=65125
- Simplifying this fraction:
P(only one subject)=65÷5125÷5=1325
Final Answer:
The probability that a student selected at random from the class has passed in only one subject is 1325.
- Let A be the event that a student passed in Mathematics.
- Let B be the event that a student passed in Statistics.
- Total number of students, n=125
- Number of students who passed in Mathematics, |A|=70
- Number of students who passed in Statistics, |B|=55
- Number of students who passed in both subjects, |A∩B|=30
- Students who passed only Mathematics can be calculated as:
|A only|=|A|−|A∩B|=70−30=40
- Students who passed only Statistics can be calculated as:
|B only|=|B|−|A∩B|=55−30=25
- The total number of students passing only one subject is:
|A only|+|B only|=40+25=65
- The probability that a student selected at random passes in only one subject is given by:
P(only one subject)=|A only|+|B only|n=65125
- Simplifying this fraction:
P(only one subject)=65÷5125÷5=1325
The probability that a student selected at random from the class has passed in only one subject is 1325.
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - MCQ
54 Videos
- PROBABILITY I BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - Comprehension
14 Videos
- PROBABILITY I BOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY I EXERCISE - Exercise 9.2
19 Videos
- PROBABILITYBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITYEXERCISE - Comprehension
2 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
In a class of 125 students 70 passed in Mathematics, 55 in statistics, and 30 in both. Then find the probability that a student selected at random from the class has passed in only one subject.
View Solution100 students appeared for two examinations. 60 passed the first, 50 passed the second and 30 passed both. Find the probability that a student selected at random has passed at least one examination.
View Solution
Knowledge Check
The graph below shows the number of students who were present on Thursday from each of the 5 groups in Ms. Meagan's class. What is the probability that a student selected at random from the class on Thrusday is in Group 4?
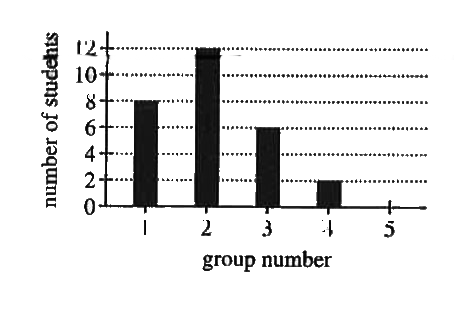 A128B114C15D14
A128B114C15D14
100 students appeared for two examinations .60 passed the first , 50 passed the second and 30 passed both . Find the probability that a student selected at random has failed in both examinations .
View SolutionIn a class of 60 students, 30 students like Mathematics, 25 like Science and 15 like both. Then, the number of students who like either Mathematics or Science is
View SolutionIn a school 25% students are failed in Mathematics, 15% in Physics and 5% students fail in both Mathematics and Physics. A student is selected at random.
(i) If he is fail in Physics, find the probability that he is fail in Mathematics.
(ii) If he is fail in Mathematics, find the probability that he in fail in Physics.
(iii) Find the probability that he is fail either in Mathematics or in Physics.
View SolutionIn class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both mathematics and biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology or both.
View SolutionIn Class XI of a school 40% of the students study Mathematics and 30% study Biology. 10% of the class study both Mathematics and Biology. If a student is selected at random from the class, find the probability that he will be studying Mathematics or Biology.
View SolutionIn a class of 50 students, 20 are boys and rest are girls. A student is selected at random. Find the probability of selecting a boy.
View SolutionTwo thirds of the students in a class are boys and the rest girls. It is known that the probability of a girl getting a first class is 0.25 and that of a boy getting a first class is 0.28. find the probability that a student chosen at random will get first class marks in the subject.
View Solution
