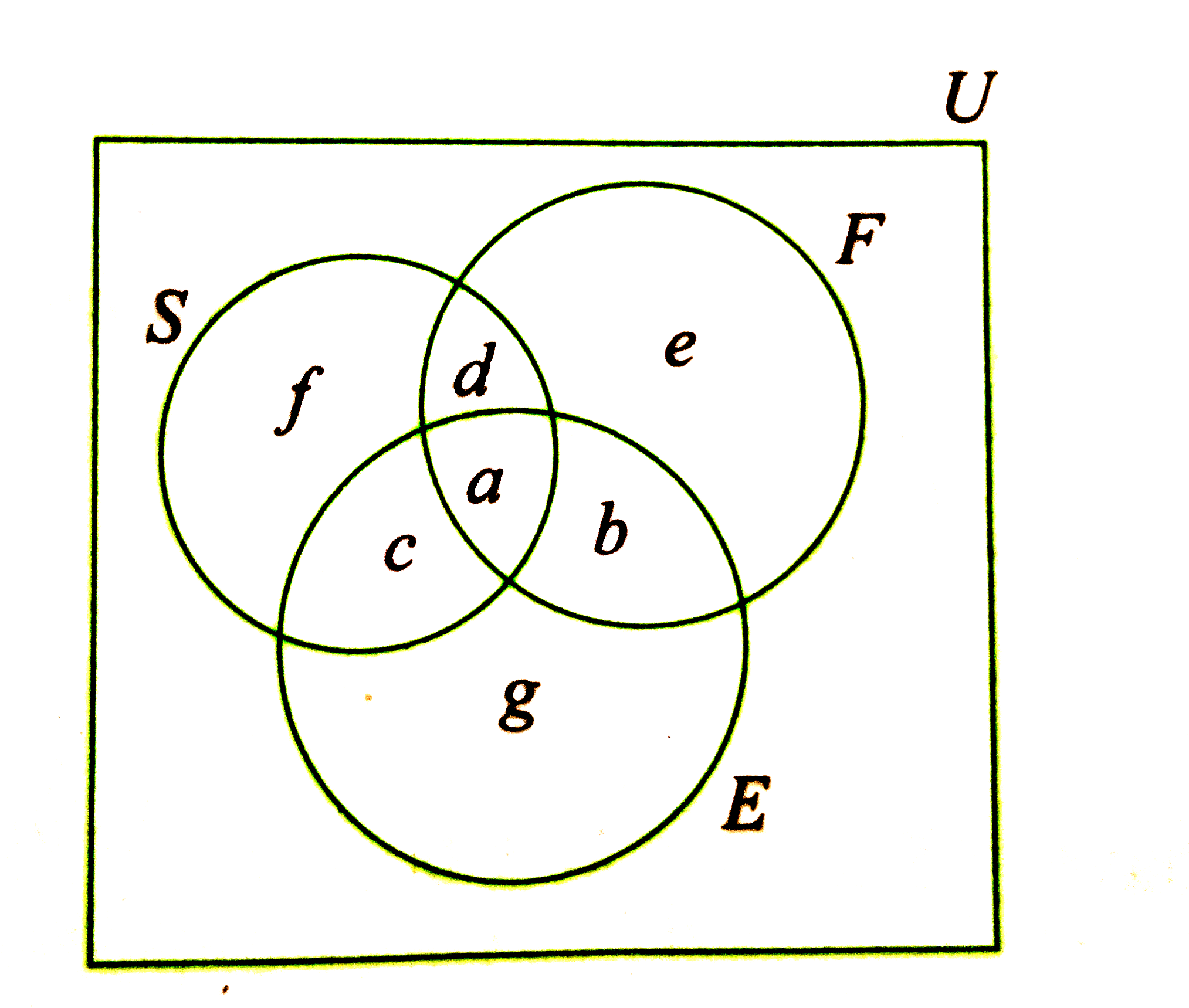
In a group of 50 students, the number of students studying French, English, Sanskrit were found to be as follows French = 17, English = 13, Sanskrit = 15 French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English , French and Sanskrit = 3. Find the number of students who study
(i) only French, (ii) only English.
(iii) only Sanskrit. , (iv) English and Sanskrit but not French.
(v) French and Sanskrit but not English.
(vi) French and English but not Sanskrit.
(vii) atleast one of the three languages.
(viii) none of the three languages.
To solve the problem step by step, we will use the information provided about the number of students studying French, English, and Sanskrit, as well as their intersections.
Given Data:
- Total students = 50
- Students studying French (F) = 17
- Students studying English (E) = 13
- Students studying Sanskrit (S) = 15
- Students studying both French and English (F ∩ E) = 9
- Students studying both English and Sanskrit (E ∩ S) = 4
- Students studying both French and Sanskrit (F ∩ S) = 5
- Students studying all three languages (F ∩ E ∩ S) = 3
Step 1: Define Variables
Let:
- A = Students studying only French
- B = Students studying only Sanskrit
- C = Students studying only English
- D = Students studying French and Sanskrit but not English
- E = Students studying French and English but not Sanskrit
- F = Students studying English and Sanskrit but not French
- G = Students studying all three languages
Step 2: Set Up Equations
From the given data, we can set up the following equations:
1. For French:
A+E+D+G=17 (1)
2. For English:
C+E+F+G=13 (2)
3. For Sanskrit:
B+D+F+G=15 (3)
4. For French and English:
E+G=9 (4)
5. For English and Sanskrit:
F+G=4 (5)
6. For French and Sanskrit:
D+G=5 (6)
7. For all three languages:
G=3 (7)
Step 3: Substitute G in Equations
From equation (7), substitute G=3 into equations (4), (5), and (6):
- From (4):
E+3=9
E=6 (8)
- From (5):
F+3=4
F=1 (9)
- From (6):
D+3=5
D=2 (10)
Step 4: Substitute E, F, D, and G into Equations
Now substitute E,F,D, and G into equations (1), (2), and (3):
- From (1):
A+6+2+3=17
A+11=17
A=6 (11)
- From (2):
C+6+1+3=13
C+10=13
C=3 (12)
- From (3):
B+2+1+3=15
B+6=15
B=9 (13)
Step 5: Summary of Students
Now we have:
- Students studying only French (A) = 6
- Students studying only English (C) = 3
- Students studying only Sanskrit (B) = 9
- Students studying French and Sanskrit but not English (D) = 2
- Students studying English and Sanskrit but not French (F) = 1
- Students studying French and English but not Sanskrit (E) = 6
- Students studying all three languages (G) = 3
Step 6: Calculate Total Students Studying At Least One Language
To find the number of students studying at least one language, we sum all the unique groups:
A+B+C+D+E+F+G=6+9+3+2+6+1+3=30
Step 7: Calculate Students Studying None of the Languages
To find the number of students studying none of the languages:
None=Total Students−At least one=50−30=20
Final Answers:
(i) Only French = 6
(ii) Only English = 3
(iii) Only Sanskrit = 9
(iv) English and Sanskrit but not French = 1
(v) French and Sanskrit but not English = 2
(vi) French and English but not Sanskrit = 6
(vii) At least one of the three languages = 30
(viii) None of the three languages = 20
- Total students = 50
- Students studying French (F) = 17
- Students studying English (E) = 13
- Students studying Sanskrit (S) = 15
- Students studying both French and English (F ∩ E) = 9
- Students studying both English and Sanskrit (E ∩ S) = 4
- Students studying both French and Sanskrit (F ∩ S) = 5
- Students studying all three languages (F ∩ E ∩ S) = 3
Let:
- A = Students studying only French
- B = Students studying only Sanskrit
- C = Students studying only English
- D = Students studying French and Sanskrit but not English
- E = Students studying French and English but not Sanskrit
- F = Students studying English and Sanskrit but not French
- G = Students studying all three languages
From the given data, we can set up the following equations:
A+E+D+G=17 (1)
C+E+F+G=13 (2)
B+D+F+G=15 (3)
E+G=9 (4)
F+G=4 (5)
D+G=5 (6)
G=3 (7)
From equation (7), substitute G=3 into equations (4), (5), and (6):
E+3=9
E=6 (8)
F+3=4
F=1 (9)
D+3=5
D=2 (10)
Now substitute E,F,D, and G into equations (1), (2), and (3):
A+6+2+3=17
A+11=17
A=6 (11)
C+6+1+3=13
C+10=13
C=3 (12)
B+2+1+3=15
B+6=15
B=9 (13)
Now we have:
- Students studying only French (A) = 6
- Students studying only English (C) = 3
- Students studying only Sanskrit (B) = 9
- Students studying French and Sanskrit but not English (D) = 2
- Students studying English and Sanskrit but not French (F) = 1
- Students studying French and English but not Sanskrit (E) = 6
- Students studying all three languages (G) = 3
To find the number of students studying at least one language, we sum all the unique groups:
A+B+C+D+E+F+G=6+9+3+2+6+1+3=30
To find the number of students studying none of the languages:
None=Total Students−At least one=50−30=20
(i) Only French = 6
(ii) Only English = 3
(iii) Only Sanskrit = 9
(iv) English and Sanskrit but not French = 1
(v) French and Sanskrit but not English = 2
(vi) French and English but not Sanskrit = 6
(vii) At least one of the three languages = 30
(viii) None of the three languages = 20
Topper's Solved these Questions
- SETSBOOK - NCERT EXEMPLARCHAPTER - SETSEXERCISE - OBJECTIVE TYPE QUESTIONS
14 Videos
- SETSBOOK - NCERT EXEMPLARCHAPTER - SETSEXERCISE - FILLERS
9 Videos
- SETSBOOK - NCERT EXEMPLARCHAPTER - SETSEXERCISE - TRUE AND FALSE
6 Videos
- SEQUENCE AND SERIESBOOK - NCERT EXEMPLARCHAPTER - SEQUENCE AND SERIESEXERCISE - Match the comumms
2 Videos
- STATISTICSBOOK - NCERT EXEMPLARCHAPTER - STATISTICSEXERCISE - FILLERS
7 Videos
Similar Questions
In a group of 50 students, the number of students learning - French, English, Sanskrit were found to be as follows: French = 17, English = 13, Sanskrit = 15, French and English = 09, English and Sanskrit = 4, French and Sanskrit = 5, English, French and Sanskrit = 3. Find the number of students who are learning at?
French only
(ii) English only
(iii) Sanskrit only
(iv) English and Sanskrit but not French
(v) French and Sanskrit but not English
(vi) French and English but not Sanskrit
(vii) at least one of the three languages
(viii) none of the three languages
(ix) exactly one language (X) exactly two languages
View SolutionIn a survey of 100 students, the number of students studying the various languages were found to be: English only 18, English but not Hindi 23, English and Sanskrit 8, English 26, Sanskrit 48, Sanskrit and Hindi 8, no language 24. Find:
How many students were studying Hindi?
View Solution
Knowledge Check
Sanskrit in India today is a
AHindu languageBModern Indian languageCModern Indian language and a classical languageDReligious languageIn the class of 100 students, the number of students passed in English is 46, in Maths is 46 and in Commerce is 58. The number who passed in English and Maths is 16, Maths and commerce is 24 and English and commerce is 26, and the number who passed in all subjects is 7. Find the number of the students who failed in all subjects.
A13B8C9D7
In a survey of 100 students, the number of students studying the various languages were found to be: English only 18, English but not Hindi 23, English and Sanskrit 8, English 26, Sanskrit 48, Sanskrit and Hindi 8, no language 24. Find:
How many students were studying English and Hindi?
View SolutionAre you going ...... English and Sanskrit ? (learn)
View SolutionIn a survey of 100 students, how many of students studying the various languages were found to study: English only 18, English but not Hindi 23, English and Sanskrit 8, English 26, Sanskrit 48, Sanskrit and Hindi 8, no language 24 Find:(i) how many students were studying Hindi (ii) how many students were studying English and Hindi
View SolutionHe neither knows English nor French.
View SolutionHe knows Sanskrit.
View Solution
Find the average number of students who opted for Maths, Sociology and Sanskrit together ?
View Solution
