In a parallelogram PQRS, PX and QY are the perpendiculars drawn from P and Q respectively so SR and SR produced. Prove that PX= QY.
To prove that PX=QY in the parallelogram PQRS where PX and QY are the perpendiculars drawn from points P and Q respectively to line SR (and its extension), we can follow these steps:
1. Identify the Parallelogram:
Let PQRS be a parallelogram. By the properties of a parallelogram, we know that opposite sides are equal and parallel.
2. Draw the Perpendiculars:
Draw perpendiculars PX from point P to line SR and QY from point Q to line SR.
3. Identify the Triangles:
We will consider triangles △PXS and △QYR.
4. Show that Opposite Sides are Equal:
Since PQRS is a parallelogram, we have:
PS=QR
(Opposite sides of a parallelogram are equal.)
5. Show that Angles are Equal:
- Since PS is parallel to QR and SR is a transversal, we have:
∠PSX=∠QRY(corresponding angles)
- Also, since PX and QY are perpendicular to SR, we have:
∠PXS=90∘and∠QYR=90∘
6. Apply AAS Congruence:
Now, we have:
- PS=QR (sides)
- ∠PSX=∠QRY (angles)
- ∠PXS=∠QYR=90∘ (angles)
By the Angle-Angle-Side (AAS) criterion, we can conclude that:
△PXS≅△QYR
7. Conclude with CPCT:
Since the triangles are congruent, we have:
PX=QY(by Corresponding Parts of Congruent Triangles)
Final Statement:
Thus, we have proved that PX=QY.
---
Let PQRS be a parallelogram. By the properties of a parallelogram, we know that opposite sides are equal and parallel.
Draw perpendiculars PX from point P to line SR and QY from point Q to line SR.
We will consider triangles △PXS and △QYR.
Since PQRS is a parallelogram, we have:
PS=QR
(Opposite sides of a parallelogram are equal.)
- Since PS is parallel to QR and SR is a transversal, we have:
∠PSX=∠QRY(corresponding angles)
- Also, since PX and QY are perpendicular to SR, we have:
∠PXS=90∘and∠QYR=90∘
Now, we have:
- PS=QR (sides)
- ∠PSX=∠QRY (angles)
- ∠PXS=∠QYR=90∘ (angles)
△PXS≅△QYR
Since the triangles are congruent, we have:
PX=QY(by Corresponding Parts of Congruent Triangles)
Thus, we have proved that PX=QY.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
PQRS is a parallelogram. PX and QY are respectively, the perpendiculars from P and Q to SR and RS produced. Prove that PX=QY.
View SolutionPQRS is a parallelogram. PX and QY are respectively, the perpendiculars from P and Q to SR and RS produced. Prove that PX=QY
View SolutionIn Figure, AD is a median and BL,CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM. Figure
View SolutionIn Figure, AD is a median and BL, CM are perpendiculars drawn from B and C respectively on AD and AD produced. Prove that BL=CM
View SolutionPQRS is a parallelogram. RA and RB are perpendiculars from R on PQ and PS, respectively. If RA = 15 cm, RB = 22 cm, and QR = 26 cm, find PQ.
View SolutionAB is a diameter of a circle. AHandBK are perpendiculars from A and B respectively to the tangent at P Prove that AH+BK=AB.
View SolutionLet ABC be a triangle with incentre I. If P and Q are the feet of the perpendiculars from A to BI and CI, respectively, then prove that APBI+AQCl=cot.A2
View SolutionABCD is a parallelogram. Two points P and Q are taken on sides AD and BC respectively such that AP 13ADandCQ=13BC. Prove that □AQCP is a parallelogram.
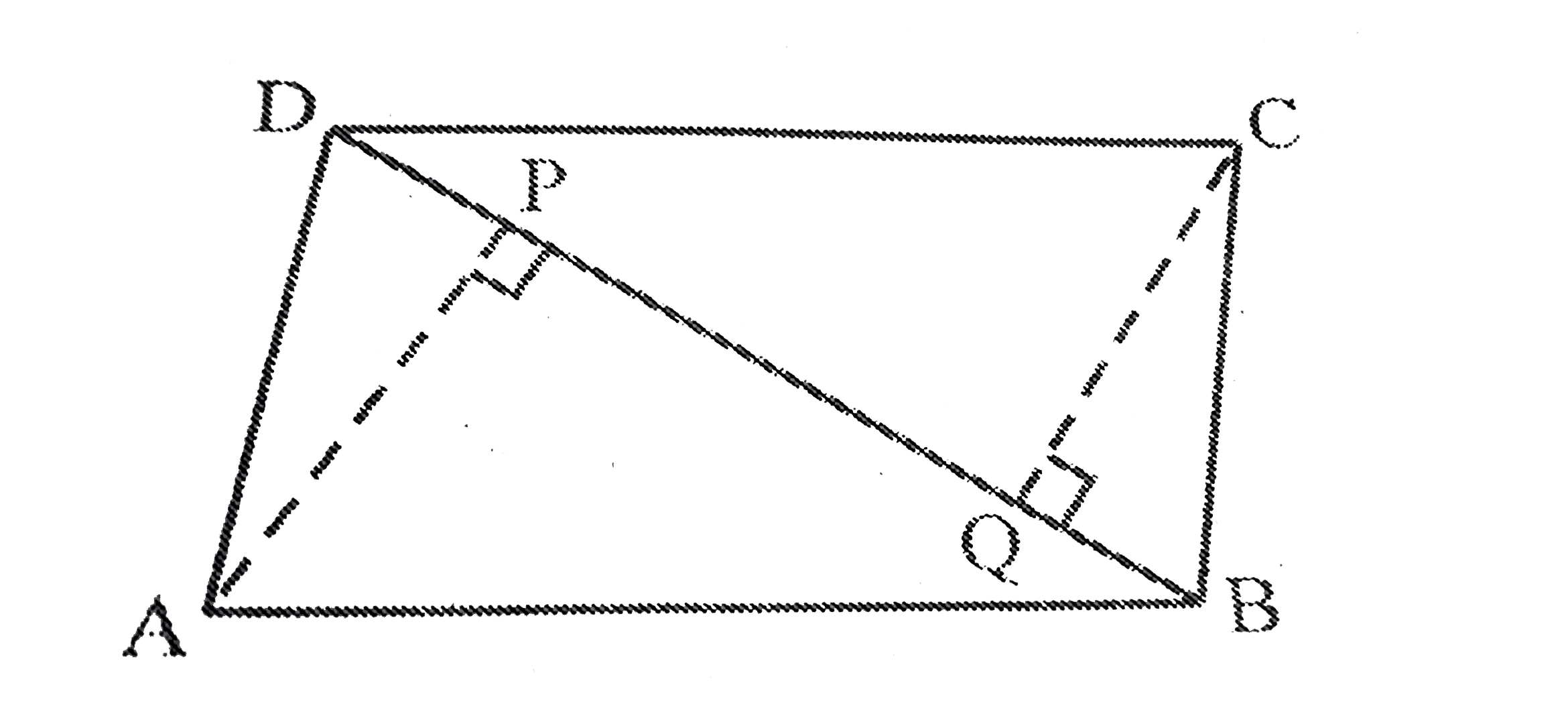
View SolutionABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD . Show that
(i) ΔAPB≅ ΔCQD
(ii) AP = CQ
View SolutionIn parallelogram PQRS. L is mid-point of side SR and SN is drawn parallel to LQ which meets RQ produced prove that :
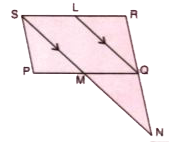
SP=12RN
View Solution
