PQRS is a parallelogram. RA and RB are perpendiculars from R on PQ and PS, respectively. If RA = 15 cm, RB = 22 cm, and QR = 26 cm, find PQ.
The correct Answer is:27 cm
To find the length of PQ in the parallelogram PQRS, we can use the area of the parallelogram calculated using two different pairs of base and height. Here’s the step-by-step solution:
Step 1: Understand the problem
We have a parallelogram PQRS with perpendiculars RA and RB from point R to sides PQ and PS, respectively. We know the lengths of these perpendiculars and one side of the parallelogram.
Step 2: Write down the known values
- RA (height from R to PQ) = 15 cm
- RB (height from R to PS) = 22 cm
- QR (length of side PS) = 26 cm
- We need to find PQ.
Step 3: Use the area formula for the parallelogram
The area of a parallelogram can be calculated using two different pairs of base and height:
1. Area using base PQ and height RA:
Area=PQ×RA
2. Area using base PS and height RB:
Area=PS×RB
Since both expressions represent the same area, we can set them equal to each other:
PQ×RA=PS×RB
Step 4: Substitute the known values into the equation
Substituting the known values into the equation:
PQ×15=26×22
Step 5: Calculate the right side of the equation
Calculate 26×22:
26×22=572
So, we have:
PQ×15=572
Step 6: Solve for PQ
To find PQ, divide both sides by 15:
PQ=57215
Step 7: Perform the division
Calculating 572÷15:
PQ=38.13 cm (approximately)
Final Answer:
The length of PQ is approximately 38.13 cm.
---
We have a parallelogram PQRS with perpendiculars RA and RB from point R to sides PQ and PS, respectively. We know the lengths of these perpendiculars and one side of the parallelogram.
- RA (height from R to PQ) = 15 cm
- RB (height from R to PS) = 22 cm
- QR (length of side PS) = 26 cm
- We need to find PQ.
The area of a parallelogram can be calculated using two different pairs of base and height:
1. Area using base PQ and height RA:
Area=PQ×RA
2. Area using base PS and height RB:
Area=PS×RB
PQ×RA=PS×RB
Substituting the known values into the equation:
PQ×15=26×22
Calculate 26×22:
26×22=572
So, we have:
PQ×15=572
To find PQ, divide both sides by 15:
PQ=57215
Calculating 572÷15:
PQ=38.13 cm (approximately)
The length of PQ is approximately 38.13 cm.
Topper's Solved these Questions
Similar Questions
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm, find the length of PB.
View SolutionPQRS is a parallelogram with ST perpendicular to PQ. Given area of Δ PST = 54 sq.cm, QS = 13 cm, and TQ = 5 cm, find the perimeter of the parallelogram.
View SolutionIn ΔABC, perpendiculars AP and CQ are droped from vertices A and C on opposite sides BC and AB, respectively. If AB=10cm,BC=16cm,AP=8.8cm, find PQ .
View SolutionIn figure, ABCD is a parallelogram, AE perpendicular to DC and CF perpendicular to AD. If AB = 16cm, AE = 8cm and CF = 10cm, Find AD.
View SolutionPQRS is a parallelogram with PQ=15cm,ST=10cm,andQV=12cm. Find PS.
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
View SolutionIn the given figure, PQ//AB, CQ = 4.8 cm QB = 3.6 cm and AB = 6-3 cm. Find :

PQ
View SolutionPQRS is a parallelogram (Fig11.23).QM is the height from Q to SRandQN is the height from Q to PS. If SR=12cmandQM=8cm. Find : (a)theareaoftheparal≤gramPQRS(b)QN,ifPS=8cm
View SolutionFind the perimeter of a parallelogram whose adjacent sides measure 15 cm and 12 cm, respectively.
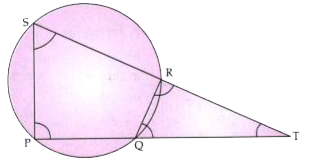
View SolutionIn the given figure PQRS is a cyclic quadrilateral PQ and SR produced meet at T.
(ii) Find SP if TP = 18 cm, RQ = 4 cm and TR = 6 cm.
View Solution
