In a quadrilateral PQRS: ∠P=80∘,∠Q=90∘,∠R=65∘. Find the measure of ∠S. Is it a convex or concave quadrilateral?
To solve the problem, we need to find the measure of angle S in quadrilateral PQRS, given the measures of angles P, Q, and R. We also need to determine whether the quadrilateral is convex or concave.
1. Understand the Sum of Angles in a Quadrilateral:
The sum of all interior angles in a quadrilateral is always 360 degrees. This can be expressed as:
∠P+∠Q+∠R+∠S=360∘
2. Substitute the Known Angles:
We know:
- ∠P=80∘
- ∠Q=90∘
- ∠R=65∘
Substitute these values into the equation:
80∘+90∘+65∘+∠S=360∘
3. Calculate the Sum of the Known Angles:
First, add the known angles together:
80∘+90∘+65∘=235∘
4. Solve for Angle S:
Now, substitute this sum back into the equation:
235∘+∠S=360∘
To find ∠S, subtract 235 degrees from both sides:
∠S=360∘−235∘=125∘
5. Determine the Type of Quadrilateral:
A quadrilateral is considered concave if at least one of its angles is greater than 180 degrees. Conversely, if all angles are less than 180 degrees, it is convex. In this case, we see:
- ∠S=125∘ (which is less than 180 degrees)
- ∠P=80∘
- ∠Q=90∘
- ∠R=65∘
Since all angles are less than 180 degrees, we conclude that quadrilateral PQRS is convex.
Final Answer:
- Measure of angle S: 125∘
- Type of quadrilateral: Convex
The sum of all interior angles in a quadrilateral is always 360 degrees. This can be expressed as:
∠P+∠Q+∠R+∠S=360∘
We know:
- ∠P=80∘
- ∠Q=90∘
- ∠R=65∘
80∘+90∘+65∘+∠S=360∘
First, add the known angles together:
80∘+90∘+65∘=235∘
Now, substitute this sum back into the equation:
235∘+∠S=360∘
To find ∠S, subtract 235 degrees from both sides:
∠S=360∘−235∘=125∘
A quadrilateral is considered concave if at least one of its angles is greater than 180 degrees. Conversely, if all angles are less than 180 degrees, it is convex. In this case, we see:
- ∠S=125∘ (which is less than 180 degrees)
- ∠P=80∘
- ∠Q=90∘
- ∠R=65∘
- Measure of angle S: 125∘
- Type of quadrilateral: Convex
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBook:MTG IIT JEE FOUNDATIONChapter:UNDERSTANDING QUADRILATERALSExercise:NCERT SECTION (EXERCISE 3.1)
Explore 7 Videos
- UNDERSTANDING QUADRILATERALSBook:MTG IIT JEE FOUNDATIONChapter:UNDERSTANDING QUADRILATERALSExercise:NCERT SECTION (EXERCISE 3.2)
Explore 6 Videos
- UNDERSTANDING QUADRILATERALSBook:MTG IIT JEE FOUNDATIONChapter:UNDERSTANDING QUADRILATERALSExercise:OLYMPAID/HOTS CORNER
Explore 11 Videos
- SQUARES AND SQUARE ROOTSBook:MTG IIT JEE FOUNDATIONChapter:SQUARES AND SQUARE ROOTSExercise:Olympiad/HOTS Corner
Explore 20 Videos
- VISUALISING SOLID SHAPESBook:MTG IIT JEE FOUNDATIONChapter:VISUALISING SOLID SHAPESExercise:OLYMPIAD/HOTS CORNER
Explore 10 Videos
Similar Questions
Knowledge Check
In cyclic quadrilateral PQRS, 7∠P=2∠R Then,∠P=
A20∘B40∘C140∘D100∘Three angles of a quadrilateral are 54∘,80∘and116∘. Find the measure of the fourth angle.
A120∘B105∘C100∘D110∘
The measure of __________ angle of concave quadrilateral is more than 180°.
View SolutionThree angles of a quadrilateral are 75∘,90∘and75∘. Find the measure of the fourth angle.
View SolutionIn a quadrilateral PQRS, ∠P = 50°, ∠Q = 50°, ∠R = 60°. Find ∠S. Is this quadrilateral convex or concave?
View SolutionIn ΔPQR,∠P=40∘ and ∠Q=60∘. Find ∠R
View SolutionIn quadrilateral PQRS,P:Q:R:S=3:5:9:7. Find all the angles of quadrilateral PQRS.
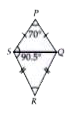
View SolutionPQRS is a kite.If ∠P=70∘ and ∠S=90.5∘,then ∠R equals
View Solution
