In a rhombus ABCD if ∠ACB=40∘, then fine ∠ADC.
The correct Answer is:100∘
To solve the problem, we need to find the angle ∠ADC in rhombus ABCD given that ∠ACB=40∘.
1. Identify the properties of the rhombus:
- In a rhombus, all sides are equal, and the opposite angles are equal.
2. Recognize triangle ABC:
- Since ABCD is a rhombus, triangles ABC and ACB are isosceles because AB=AC (sides of the rhombus).
3. Set up the angles in triangle ABC:
- We know that ∠ACB=40∘.
- Let ∠CAB=∠ABC=x (since ABC is isosceles).
4. Use the triangle angle sum property:
- The sum of angles in triangle ABC is 180∘:
∠CAB+∠ABC+∠ACB=180∘
Substituting the known values:
x+x+40∘=180∘
This simplifies to:
2x+40∘=180∘
5. Solve for x:
- Rearranging gives:
2x=180∘−40∘
2x=140∘
x=70∘
- Therefore, ∠CAB=∠ABC=70∘.
6. Find ∠ADC:
- Since opposite angles in a rhombus are equal, we have:
∠ADC=∠ABC=70∘
Final Answer:
Thus, ∠ADC=100∘.
- In a rhombus, all sides are equal, and the opposite angles are equal.
- Since ABCD is a rhombus, triangles ABC and ACB are isosceles because AB=AC (sides of the rhombus).
- We know that ∠ACB=40∘.
- Let ∠CAB=∠ABC=x (since ABC is isosceles).
- The sum of angles in triangle ABC is 180∘:
∠CAB+∠ABC+∠ACB=180∘
Substituting the known values:
x+x+40∘=180∘
This simplifies to:
2x+40∘=180∘
- Rearranging gives:
2x=180∘−40∘
2x=140∘
x=70∘
- Therefore, ∠CAB=∠ABC=70∘.
- Since opposite angles in a rhombus are equal, we have:
∠ADC=∠ABC=70∘
Thus, ∠ADC=100∘.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
Knowledge Check
A rhombus has :
Aone line of symmetryBtwo lines of symmetry eachCfour lines of symmetryDno line of symmetry
 .
.
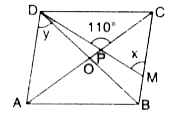
The given figure shows a rhombus ABCD in which angle BCD=80∘. Find angles x and y.
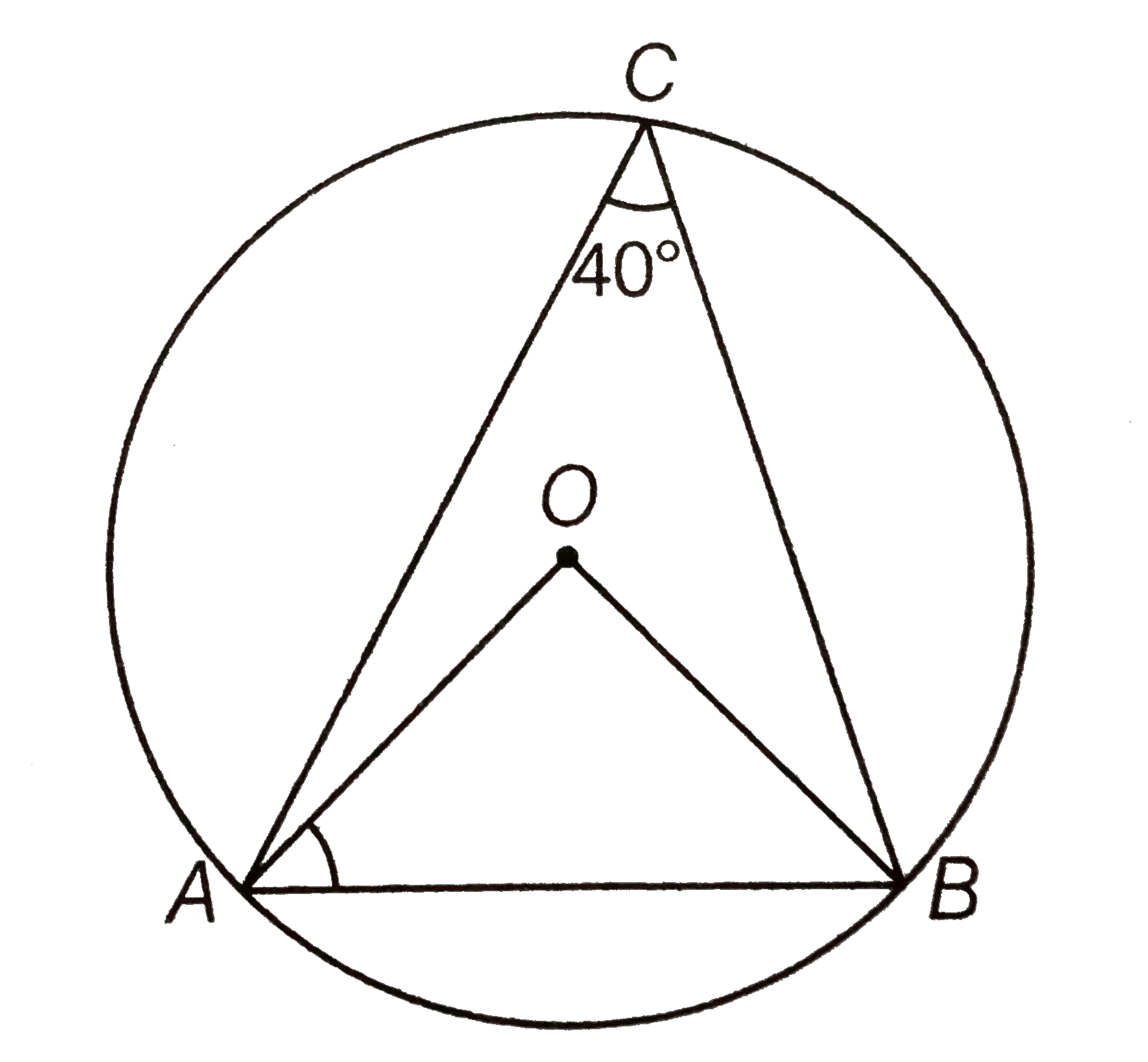
View SolutionIn figure, ∠ACB=40∘. Find ∠OAB.
View Solution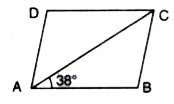
ABCD is a rhombus. If ∠BAC=38∘, find:
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.
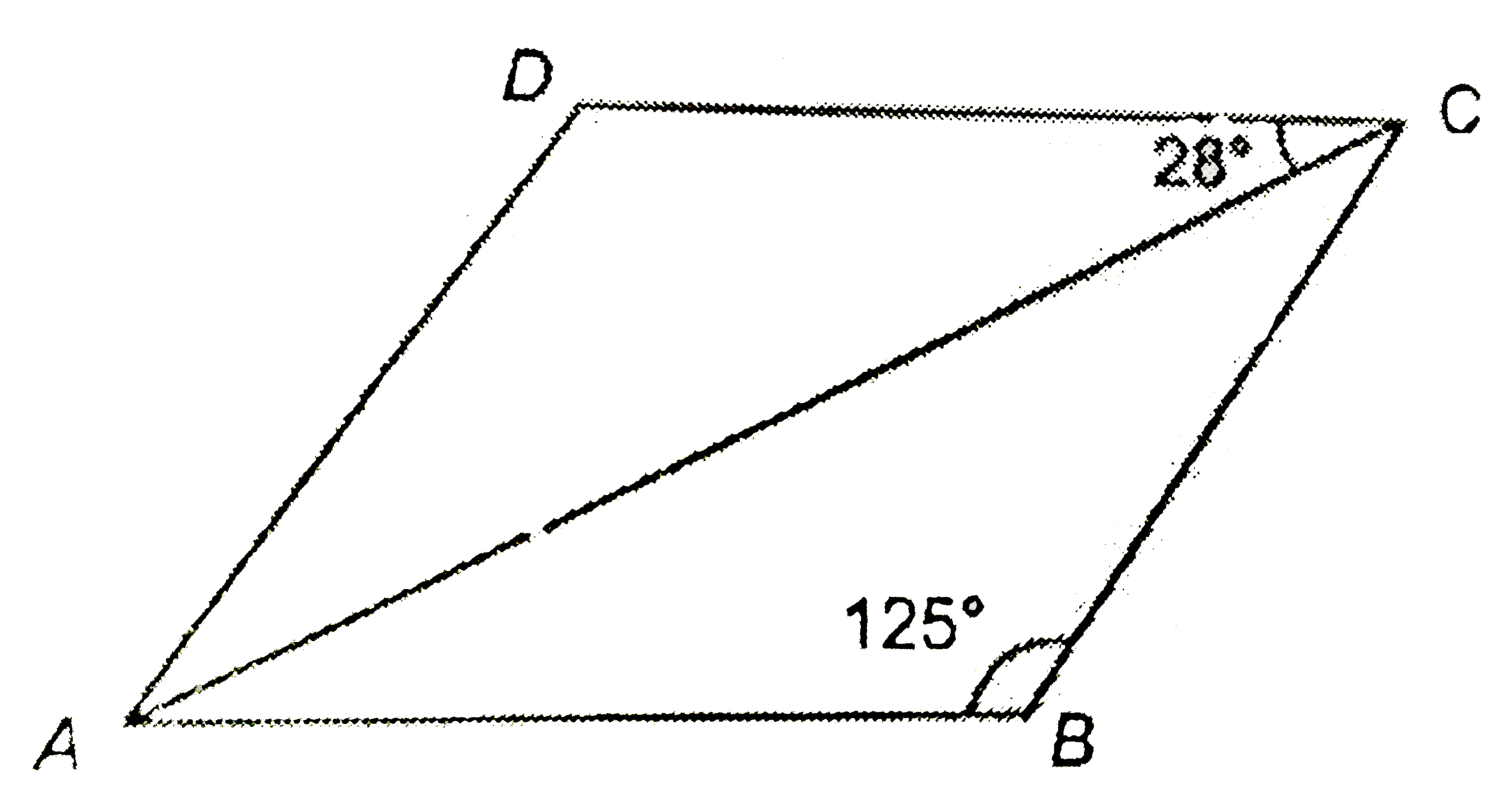
View SolutionIn the adjoining figure, ABCD is a parallelogram. If ∠ABC=125∘,
∠ACD=28∘,then fine∠DAC.
View SolutionIn the adjoining figure, O is the centre of the circle.If ∠BAC=40∘, then find the value of ∠ADC.

View SolutionIn the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
View SolutionABCD is a rhombus. If ∠BCA=35∘,and∠ADC.
View Solution