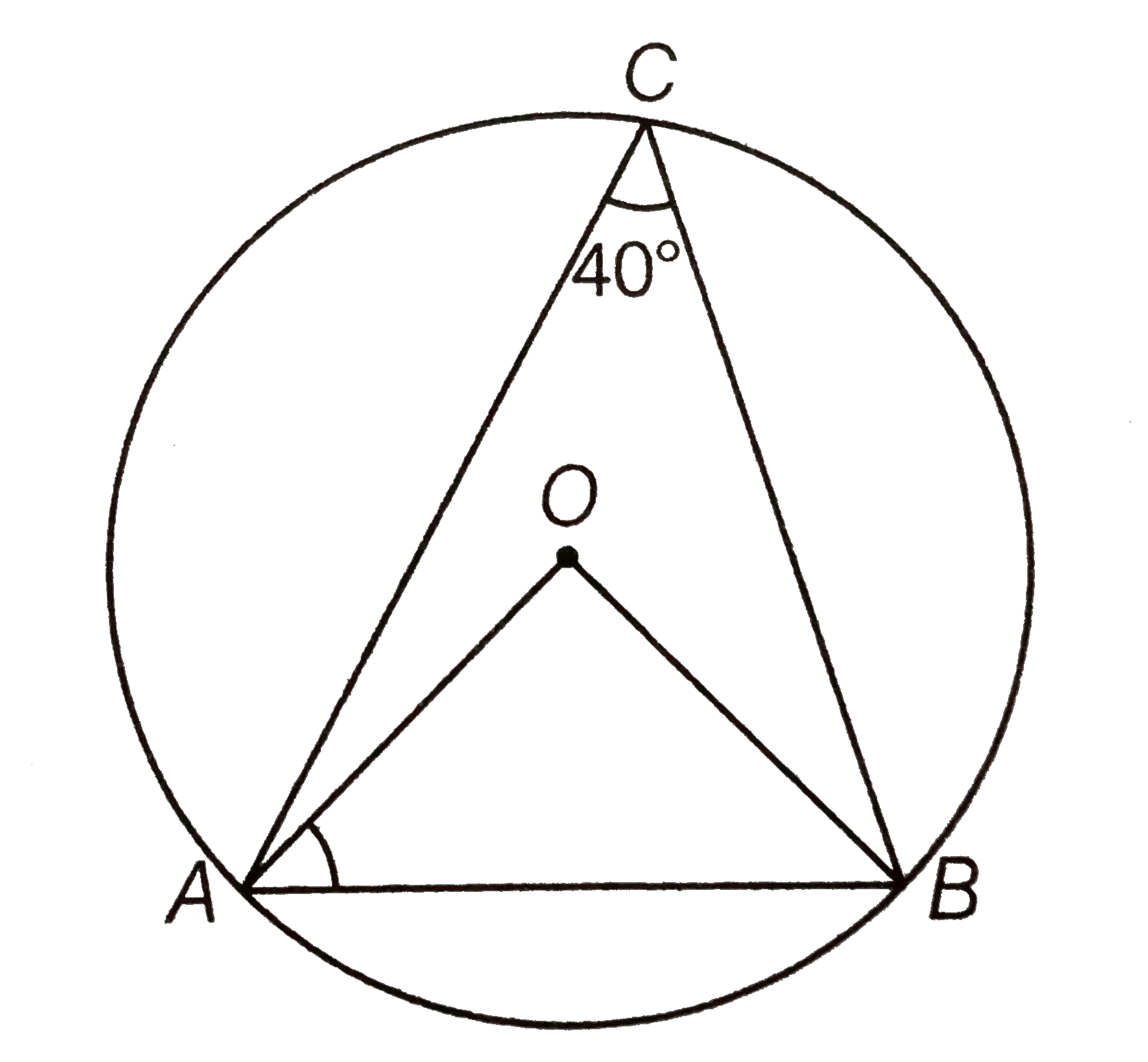
In figure, ∠ACB=40∘. Find ∠OAB.
Video Solution
Text Solution
Given, ∠ACB=40∘
We know that, a segment subtends an angle to the circle is half the angle subtends to the centre.
∴∠AOB=2∠ACB
⇒∠ACB=∠AOB2
⇒40∘=12∠AOB
⇒∠AOB=80∘ ….(i)
In ΔAOB,AO=BO [both are the radius of a circle]
⇒∠OBA=∠OAB ....(ii)
[angles opposite to the equal sides are equal]
We know that, the sum of all three angles in a triangle AOB is 180∘.
∴∠AOB+∠OBA+∠OAB=180∘
⇒80∘+∠OAB+∠OAB=180∘ [form Eqs. (i) and (ii)]
⇒2∠OAB=180∘−80∘
⇒2∠OAB=100∘
∴∠OAB=100∘2=50∘
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.4
14 Videos
- CIRCLESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise 10.2
10 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Exercise-9.4 Long Answer Type Questions
10 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
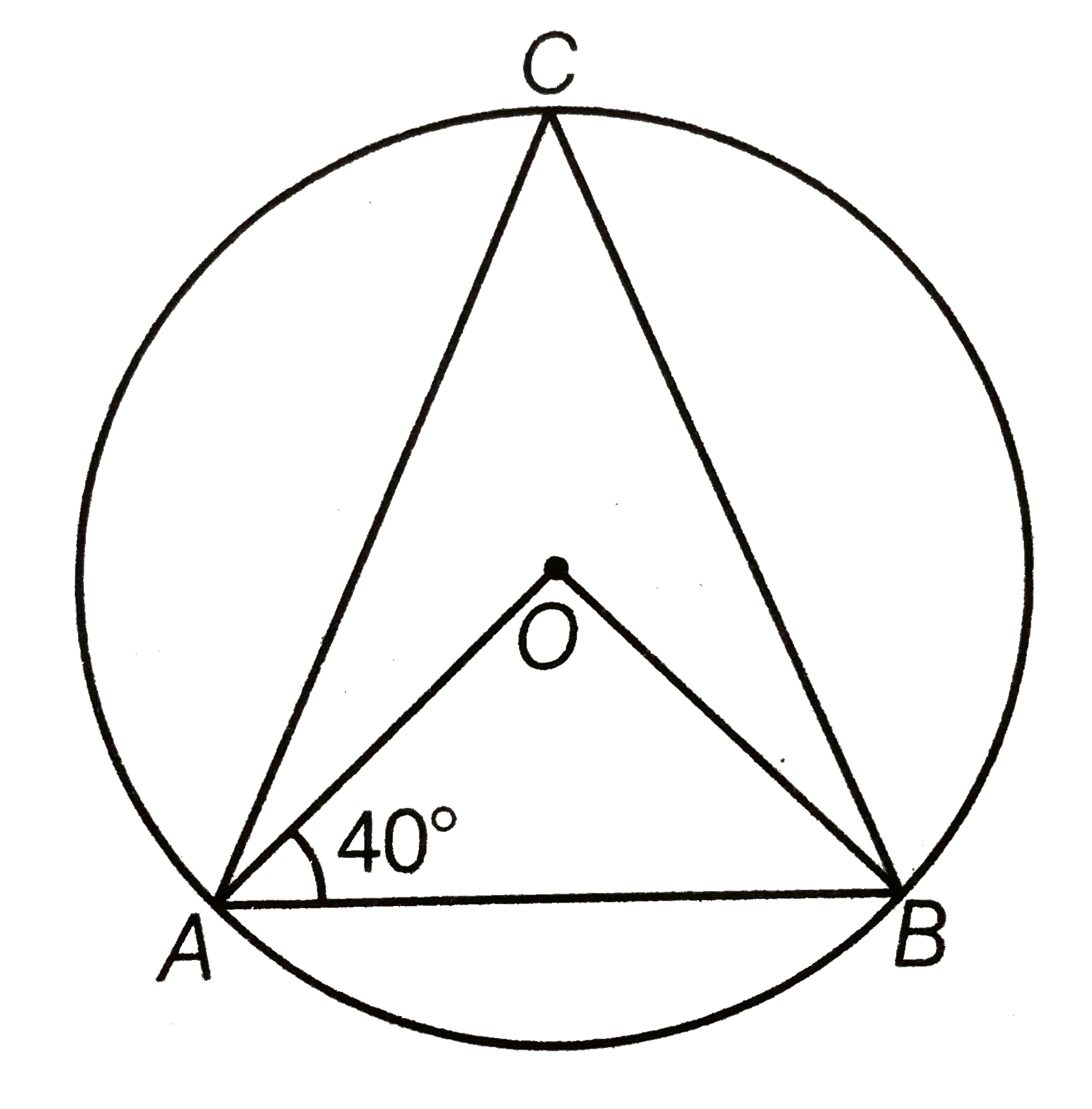
In figure, if ∠OAB=40∘,then∠ACB is equal to
View SolutionIn figure, ∠OAB=30∘and∠OCB=57∘. Find ∠BOCand∠AOC.
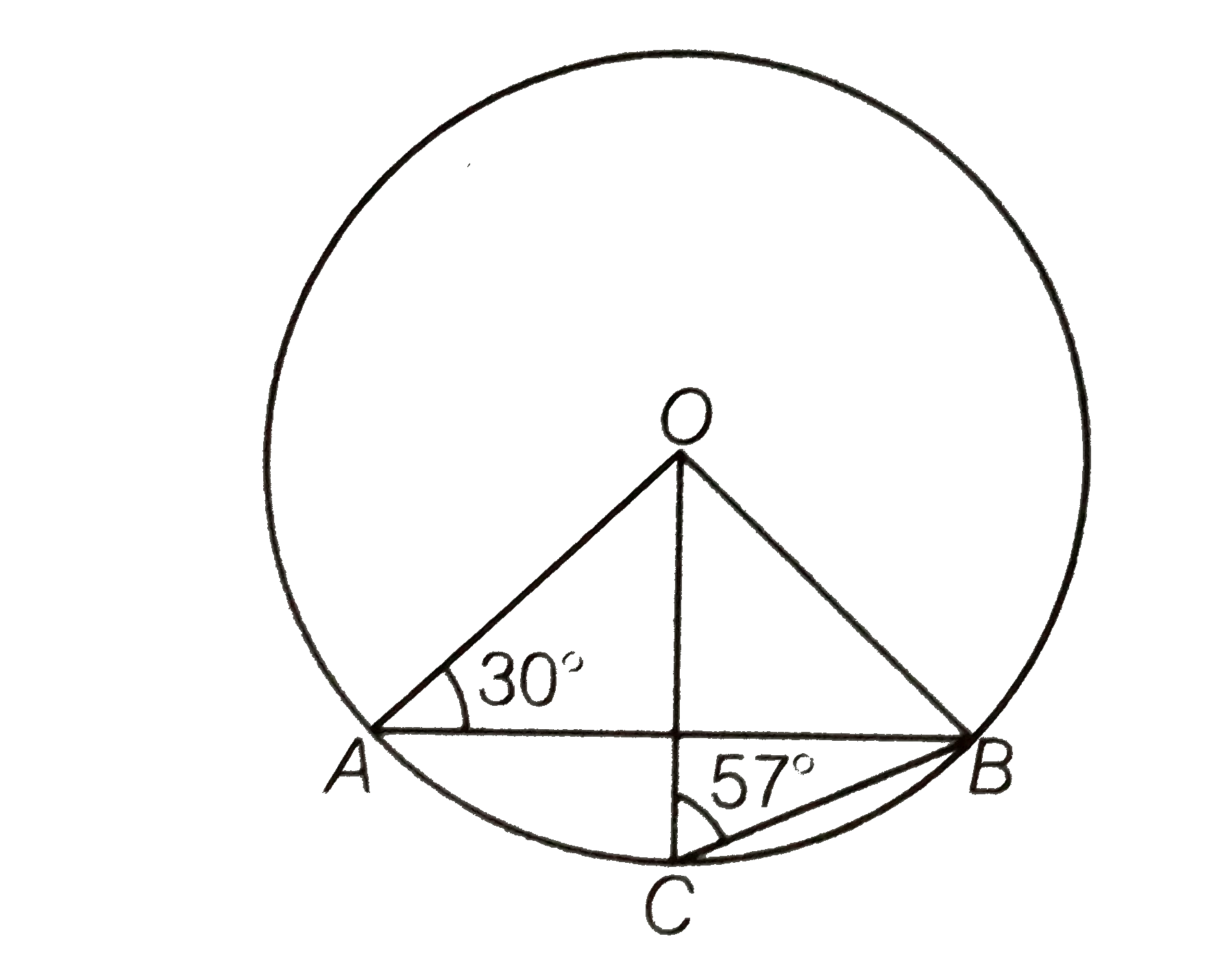
View SolutionIn the given figure, ∠OAB=30∘and∠OCB=57∘, find ∠BOCand∠AOC

View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

View SolutionIn the adjoining figure, if ∠ACB=40∘, ∠DPB=120∘, then find ∠CBD.

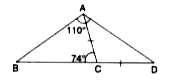
View SolutionIn the following figure ,
AC = CD, ∠BAD=110∘ and ∠ACB=74∘. Prove that : BC>CD.
View SolutionIn a rhombus ABCD if ∠ACB=40∘, then fine ∠ADC.
View SolutionABCD is a rhombus such that ∠ACB=40∘, then ∠ADB is
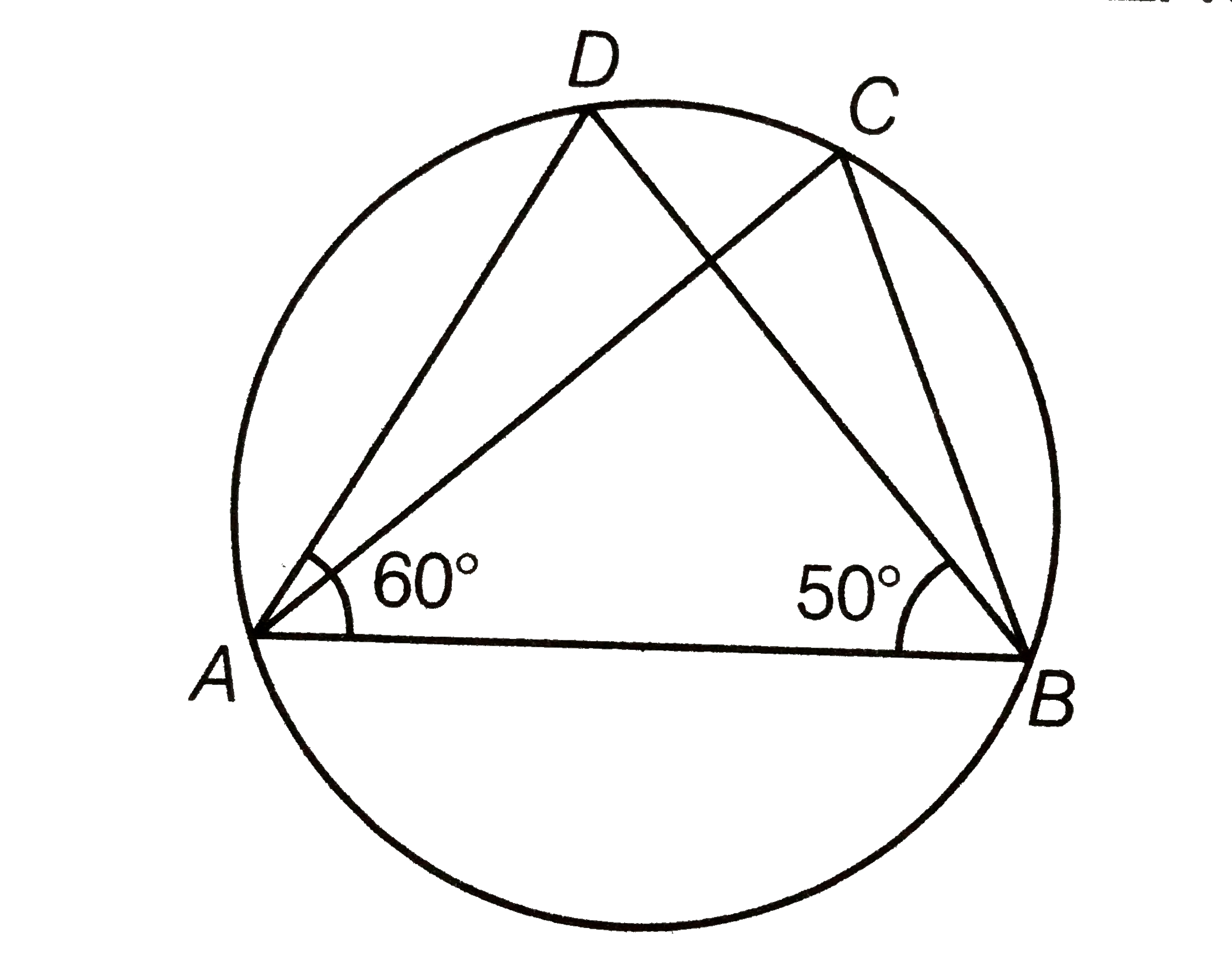
View SolutionIn figure, if ∠DAB=60∘,∠ABD=50∘,then ∠ACB is equal to
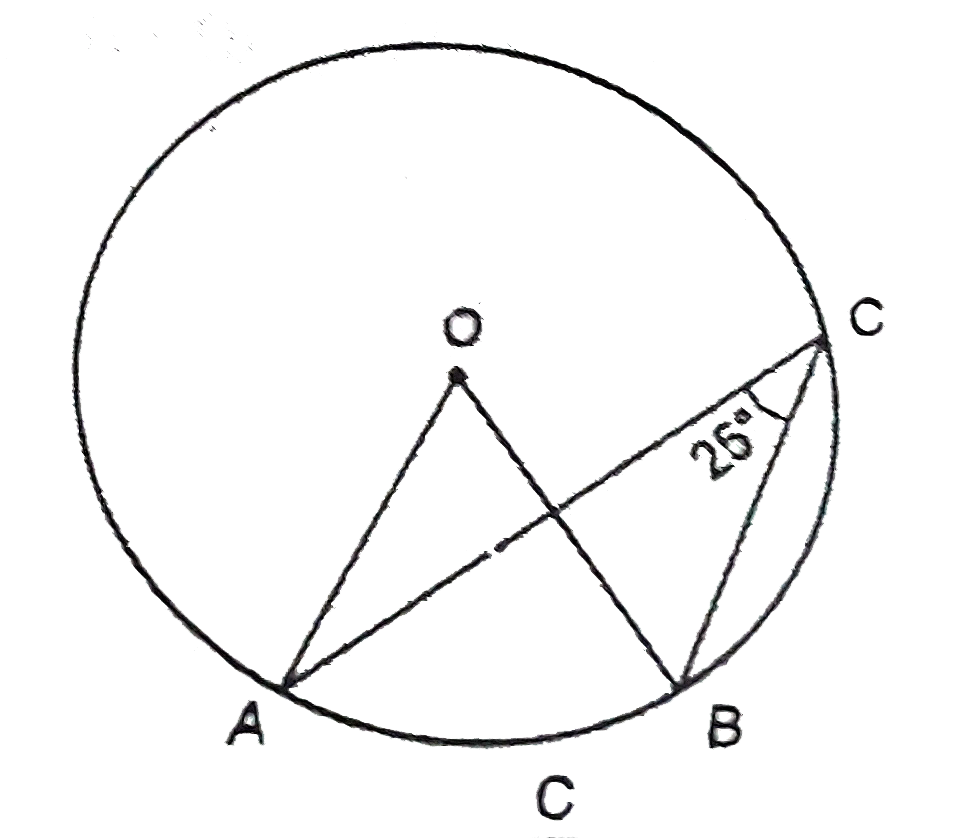
View SolutionIn the adjoining figure , O is the centre of the circle. If ∠ACB=25∘, then find ∠AOB.
View Solution
