In a survey it is found that 21 people like product A, 26 people like product B and 29 like product C. If 14 people like products A and B, 15 people like products B and C, 12 people like products C and A, and 8 people like all the three products, find
(i) how many people are surveyed in all,
(ii) how many like product C only.
To solve the problem step by step, we will use the principle of inclusion-exclusion for sets. Let's denote:
- N(A): Number of people who like product A = 21
- N(B): Number of people who like product B = 26
- N(C): Number of people who like product C = 29
- N(A∩B): Number of people who like both A and B = 14
- N(B∩C): Number of people who like both B and C = 15
- N(C∩A): Number of people who like both C and A = 12
- N(A∩B∩C): Number of people who like all three products = 8
Step 1: Calculate the total number of people surveyed
We use the formula for the union of three sets:
N(A∪B∪C)=N(A)+N(B)+N(C)−N(A∩B)−N(B∩C)−N(C∩A)+N(A∩B∩C)
Substituting the values:
N(A∪B∪C)=21+26+29−14−15−12+8
Calculating step by step:
1. Sum of individual products:
21+26+29=76
2. Sum of intersections:
14+15+12=41
3. Now substitute these into the formula:
N(A∪B∪C)=76−41+8
N(A∪B∪C)=76−41=35
N(A∪B∪C)=35+8=43
Thus, the total number of people surveyed is 43.
Step 2: Calculate the number of people who like product C only
To find the number of people who like only product C, we need to subtract those who like product C and at least one other product from the total number of people who like product C.
Using the formula:
N(C only)=N(C)−(N(A∩C)+N(B∩C)−N(A∩B∩C))
Where:
- N(A∩C) = 12 (people who like both A and C)
- N(B∩C) = 15 (people who like both B and C)
- N(A∩B∩C) = 8 (people who like all three products)
Substituting the values:
N(C only)=29−(12+15−8)
Calculating step by step:
1. Calculate the sum of intersections:
12+15=27
2. Subtract those who like all three:
27−8=19
3. Now substitute this back:
N(C only)=29−19=10
Thus, the number of people who like product C only is 10.
Summary of Results
(i) Total number of people surveyed = 43
(ii) Number of people who like product C only = 10
- N(A): Number of people who like product A = 21
- N(B): Number of people who like product B = 26
- N(C): Number of people who like product C = 29
- N(A∩B): Number of people who like both A and B = 14
- N(B∩C): Number of people who like both B and C = 15
- N(C∩A): Number of people who like both C and A = 12
- N(A∩B∩C): Number of people who like all three products = 8
N(A∪B∪C)=N(A)+N(B)+N(C)−N(A∩B)−N(B∩C)−N(C∩A)+N(A∩B∩C)
N(A∪B∪C)=21+26+29−14−15−12+8
1. Sum of individual products:
21+26+29=76
2. Sum of intersections:
14+15+12=41
3. Now substitute these into the formula:
N(A∪B∪C)=76−41+8
N(A∪B∪C)=76−41=35
N(A∪B∪C)=35+8=43
N(C only)=N(C)−(N(A∩C)+N(B∩C)−N(A∩B∩C))
- N(A∩C) = 12 (people who like both A and C)
- N(B∩C) = 15 (people who like both B and C)
- N(A∩B∩C) = 8 (people who like all three products)
N(C only)=29−(12+15−8)
1. Calculate the sum of intersections:
12+15=27
2. Subtract those who like all three:
27−8=19
3. Now substitute this back:
N(C only)=29−19=10
(i) Total number of people surveyed = 43
(ii) Number of people who like product C only = 10
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - SETSEXERCISE - EXERCISE-1A6videos
SETS
- BOOK - RS AGGARWALCHAPTER - SETSEXERCISE - EXERCISE-1B6videos
SETS
- BOOK - RS AGGARWALCHAPTER - SETSEXERCISE - OPERATIONS ON SETS (EXAMPLE)16videos
SETS
- BOOK - RS AGGARWALCHAPTER - RelationsEXERCISE - EXERCISE 2E12videos
Relations
- BOOK - RS AGGARWALCHAPTER - SOLUTION OF TRIANGLESEXERCISE - EXERCISE 18 B3videos
SOLUTION OF TRIANGLES
Similar Questions
In a survey it was found that 21 people liked product A, 26 liked product B and 29 liked product C. If 14 people liked products A and B, 12 people liked products C and A, 14 people liked products B and C and 8 liked all the three products. Find how many liked product C only.
View SolutionIn a survery, it was found that 21 persons liked product A, 26 liked product B and 29 liked product C. If 14 persons liked products A and B, 12 liked products C and A, 13 persons liked products B and C and 8 liked all the three products then
(i) Find the number of persons who liked the product C only
(ii) The number of persons who like the products A and B but not CView Solution
Knowledge Check
- Question 1 - Select One
Select the alternative that will improve the underlined part of the sentence in case there is no improvement select "no improvement".
Some people like to watches television all day.ANo improvementBlikes to watchClike to watchDLike to watching - Question 2 - Select One
He likes people to call him Sir.
AHe likes to be called Sir by people.BHe likes to be call Sir by people.CHe likes people who call him Sir.DTo call him Sir is liked by people. - Question 3 - Select One
In a school, on the Republic day, three dramas A, B and C are performed on the dais. In a group of people, who attended the function and who like at least one of the three dramas, 16 people like A,20 people like B,15 people like C,4 people like both A and B,3 people like all the three. Then how many people like at most two?
A59B41C4D6
In a survey, 50 people like product A, 30 people like product B and 20 people like product C and 35 people l not like any product like exactly two products. If 5 people like all the three products then number of people who do . [There are 100 people in survey]
View SolutionOut of 10000 people surveyed, 3700 liked city A, 4000 liked city B and 5000 liked city C. 700 people liked A and B 1200 liked B and C and 1000, liked A and C. Each person liked at least one city. Then find
The number of people liking all the three cities.View SolutionOut of 10000 people surveyed, 3700 liked city A, 4000 liked city B and 5000 liked city C. 700 people liked A and B 1200 liked A and C and 1000, liked B and C. Each person liked at least one city. Then find
The number of persons liking A and B but not C.View SolutionIn a group of 50 people , 30 like to play cricket , 25 like to play football and 32 like play hockey . Assume that each one like to play atleast one of the three games . If 15 people like to play both cricket as well as football, 11 people like to play both football well as hockey and 18 like to play both football as as hockey, then
(i) how many like to play all the three games?
(ii) how many like to play only football ?
(iii) how many like to play only hockey ?View SolutionIn the given figure, how many people like cricket and tennis both ?
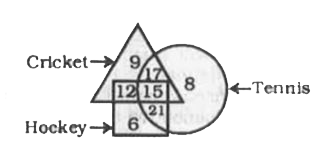 View Solution
View Solution
