In a telephone enquiry system, the number of phone calls regarding relevant enquiry follow poisson distribution with an average of five phone calls during 10-minute time intervals. The probability that there is at the most one phone call during a 10-minute time period is
The correct Answer is:D
To solve the problem, we need to find the probability that there are at most one phone call during a 10-minute time period, given that the number of phone calls follows a Poisson distribution with an average of 5 calls in that time frame.
1. Understand the Poisson Distribution:
The Poisson distribution is defined by the formula:
P(X=r)=e−mmrr!
where m is the average number of occurrences (mean), r is the number of occurrences, and e is the base of the natural logarithm (approximately equal to 2.71828).
2. Identify the Parameters:
In this problem, the average number of phone calls m=5 (given in the question).
3. Calculate Probability for r=0:
We first calculate the probability of receiving 0 calls:
P(X=0)=e−5⋅500!=e−5⋅1=e−5
4. Calculate Probability for r=1:
Next, we calculate the probability of receiving 1 call:
P(X=1)=e−5⋅511!=e−5⋅5
5. Combine the Probabilities:
To find the probability of at most one call, we sum the probabilities for 0 and 1 call:
P(X≤1)=P(X=0)+P(X=1)=e−5+5e−5
P(X≤1)=e−5(1+5)=6e−5
6. Final Result:
Therefore, the probability that there is at most one phone call during a 10-minute time period is:
P(X≤1)=6e5
Summary:
The probability that there is at most one phone call during a 10-minute time period is 6e5.
The Poisson distribution is defined by the formula:
P(X=r)=e−mmrr!
where m is the average number of occurrences (mean), r is the number of occurrences, and e is the base of the natural logarithm (approximately equal to 2.71828).
In this problem, the average number of phone calls m=5 (given in the question).
We first calculate the probability of receiving 0 calls:
P(X=0)=e−5⋅500!=e−5⋅1=e−5
Next, we calculate the probability of receiving 1 call:
P(X=1)=e−5⋅511!=e−5⋅5
To find the probability of at most one call, we sum the probabilities for 0 and 1 call:
P(X≤1)=P(X=0)+P(X=1)=e−5+5e−5
P(X≤1)=e−5(1+5)=6e−5
Therefore, the probability that there is at most one phone call during a 10-minute time period is:
P(X≤1)=6e5
The probability that there is at most one phone call during a 10-minute time period is 6e5.
Topper's Solved these Questions
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Subjective Type Questions)
15 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - ARIHANT MATHS ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
28 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
Similar Questions
If the number of telephone calls an operator receives between 10:00 am to 10:10 pm follow poisson distribution with mean 3. The probability that the operator receives one call during that interval the next day is
View SolutionSuppose that the number of telephone calls coming into a telephone exchange between 10 A.M. and 11 A.M., say, X1 is a random variable with possion distribution with parameter 2. Similarly the number of calls arriving between 11 A.M. and 12 noon, say X2 also follows a poisson distribution with parameter 6. If X1 and X2 are independent, what is the probability that more than 5 calls come in between 10 A.M. and 12 noon.
View Solution
Knowledge Check
A phone company charges 10 cents per minute for the first 3 minute of a call and 10 -c cents for each minute thereafter. What is the cost, in cents, of a 10 -minute phonecall?
A100c+70B30+7cC100−7cD100−70c
If shoppers enter a store at an average rate of r shoppers per minute and each stays in the store for an average time of T minutes, the average number of shoppers in the store, N, at any one time is given by the formula N rT = . This relationship is known as Little’s law. The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little’s law to estimate that there are 45 shoppers in the store at any time.
The owner of the Good Deals Store opens a new store across town. For the new store, the owner estimates that, during business hours, an average of 90 shoppers per hour enter the store and each of them stays an average of 12 minutes. The average number of shoppers in the new store at any time is what percent less than the average number of shoppers in the original store at any time? (Note: Ignore the percent symbol when entering your answer. For example, if the answer is 42.1%, enter 42.1)
View SolutionIf shoppers enter a store at an average rate of r shoppers per minute and each stays in the store for an average time of T minutes, the average number of shoppers in the store, N, at any one time is given by the formula N rT = . This relationship is known as Little’s law. The owner of the Good Deals Store estimates that during business hours, an average of 3 shoppers per minute enter the store and that each of them stays an average of 15 minutes. The store owner uses Little’s law to estimate that there are 45 shoppers in the store at any time.
Little’s law can be applied to any part of the store, such as a particular department or the checkout lines. The store owner determines that, during business hours, approximately 84 shoppers per hour make a purchase and each of these shoppers spend an average of 5 minutes in the checkout line. At any time during business hours, about how many shoppers, on average, are waiting in the checkout line to make a purchase at the Good Deals Store?
View SolutionThe following combination are concerned with experiments of the characterization and use of a moving coil galvanometer.
The series combination of variab resistance R, one 100Ω resistor and moving coil galvanometer is connected to a mobile phone charger having negligible internal resistance. The zero of the galvanometer lies the centre and the pointer can move 30 division full scale on either side depending on the directin of current. The reading of the galvanometer is 10 divisions and the voltages across the galvanometer and 100Ω resistor are respectively 12mV and 16 mV.
The series combination of the galvanometer with a resistnce of R is conneted across an ideal voltage supply of 12 V and this time the galvanometer shows full scale defiention of 30 divisions.
The value of R is nearly
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
In the core of nucleus fusion reactor , the gas become plasma because of
View SolutionScientists are working hard to develop nuclear fusion reactor Nuclei of heavy hydrogen, _(1)2H , known as deuteron and denoted by D, can be thought of as a candidate for fusion rector . The D−D reaction is _(1)2H+21H→12He+n+ energy. In the core of fusion reactor, a gas of heavy hydrogen of _(1)2H is fully ionized into deuteron nuclei and electrons. This collection of _12H nuclei and electrons is known as plasma . The nuclei move randomly in the reactor core and occasionally come close enough for nuclear fusion to take place. Usually , the temperature in the reactor core are too high and no material will can be used to confine the to plasma for a time t0 before the particles fly away from the core. If n is the density (number volume ) of deuterons , the productnt0is called Lawson number. In one of the criteria , a reactor is termed successful if Lawson number is greater then 5×1014s/cm2
it may be helpfull to use the following boltzmann constant
λ=8.6×10−5eV/k,e24πs0=1.44×10−9eVm
In the core of nucleus fusion reactor , the gas become plasma because of
View Solution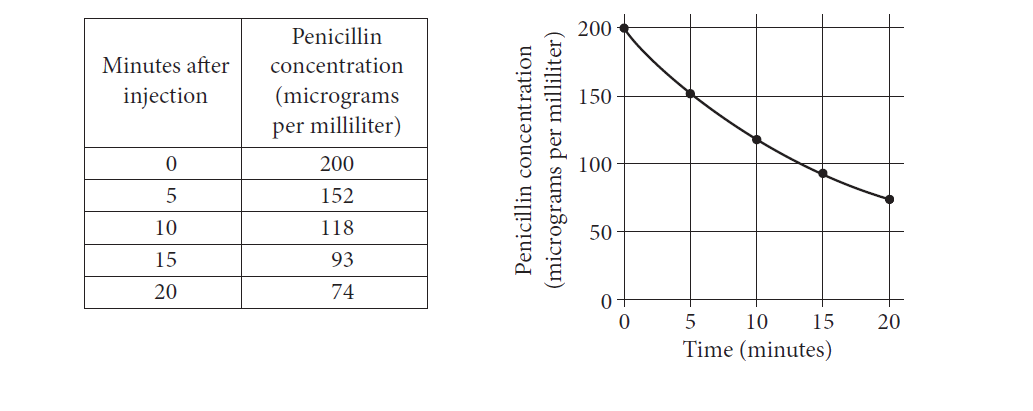
When a patient receives a penicillin injection, the kidneys begin removing the penicillin from the body. The table and graph above show the penicillin concentration in a patient’s bloodstream at 5 minute intervals for the 20 minutes immediately following a one-time penicillin injection.
According to the table, how many more micrograms of penicillin are present in 10 milliliters of blood drawn from the patient 5 minutes after the injection than are present in 8 milliliters of blood drawn 10 minutes after the injection?
View Solution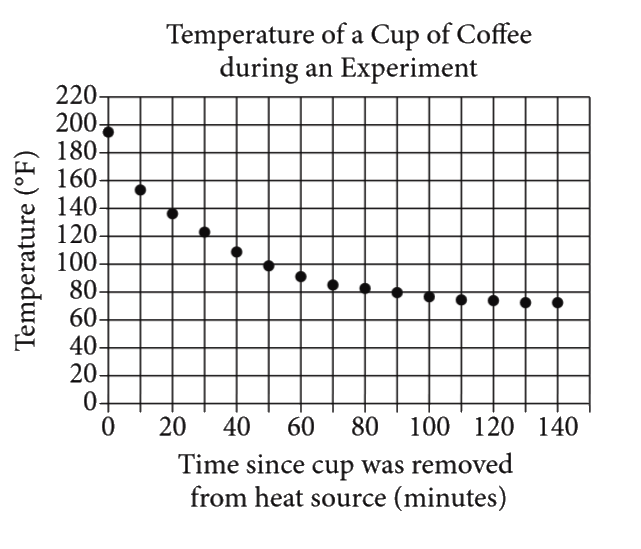
In an experiment, a heated cup of coffee is removed from a heat source, and the cup of coffee is then left in a room that is kept at a constant temperature. The graph above shows the temperature, in degrees Fahrenheit (.∘F), of the coffee immediately after being removed from the heat source and at 10-minute intervals thereafter.
During which of the following 10-minute intervals does the temperature of the coffee decrease at the greatest average rate?
View Solution
