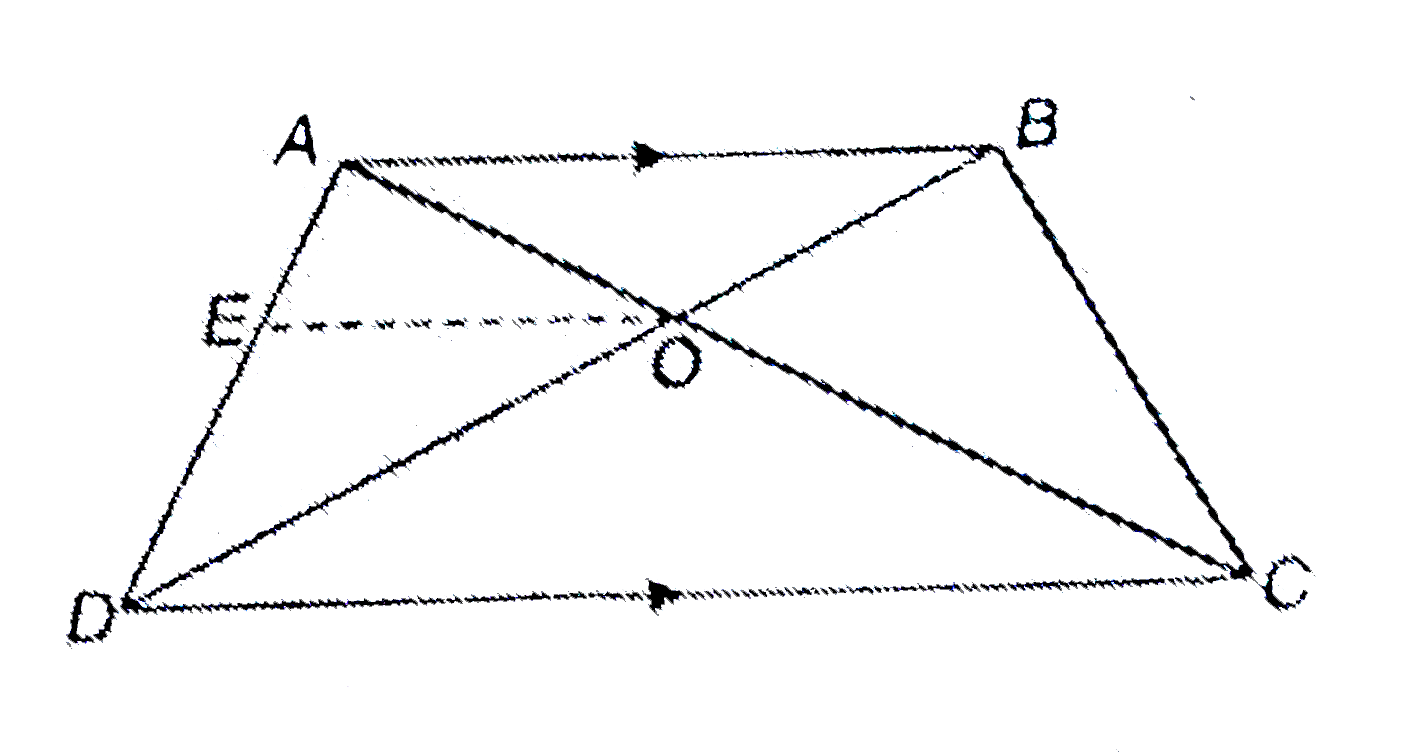
In a trapezium ABCD , it is given that AB∣∣CDandAB=2CD. Its diagonals AC and BD intersect at the point O such that ar(ΔAOB)=84cm2. Find ar(ΔCOD)
The correct Answer is:21cm2
Step by step video, text & image solution for In a trapezium ABCD , it is given that AB||CD and AB= 2CD. Its diagonals AC and BD intersect at the point O such that ar (Delta AOB)=84 cm^(2). Find ar (Delta COD) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Multiple Choice Questions (Mcq)
Explore 53 Videos
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)
Explore 1 Video
- TRIANGLESBook:RS AGGARWALChapter:TRIANGLESExercise:Exercise 7D
Explore 22 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBook:RS AGGARWALChapter:T-RATIOS OF SOME PARTICULAR ANGLESExercise:Exercise 11
Explore 27 Videos
- TRIGONOMETRIC IDENTITIESBook:RS AGGARWALChapter:TRIGONOMETRIC IDENTITIESExercise:Test Yourself
Explore 20 Videos
Similar Questions
Knowledge Check
In trapezium ABCD, AB || CD and AB = 2 CD. Its diagonals intersect at O. If the area of ΔAOB=84cm2, then the area of ΔCOD is equal to
A72cm2B21cm2C42cm2D26cm2ABCD is a trapezium in which AB∣∣CD and AB=2CD. It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A1:2B2:1C1:4D4:1ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A1:4B1:2C4:1D2:1
In a quadrilateral ABCD it is given tghat AB∣∣CD nad the diagonals ACandBD are perpendicular to each other. Show that AD.BC≥AB.CD.
View SolutionABCD is an isoceles trapezium . AB||CD AD=BC diagonal intersect at O, area of ABO = 84cm2 find area of ΔCOD
View SolutionABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
View SolutionIn the following figure, AB II CD. Diagonals AC and BD intersect at point O. If BO : OD = 1 : 3, then (area of ΔAOB)/(area of ΔABD) =
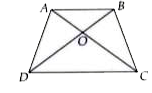
View SolutionABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
View Solution