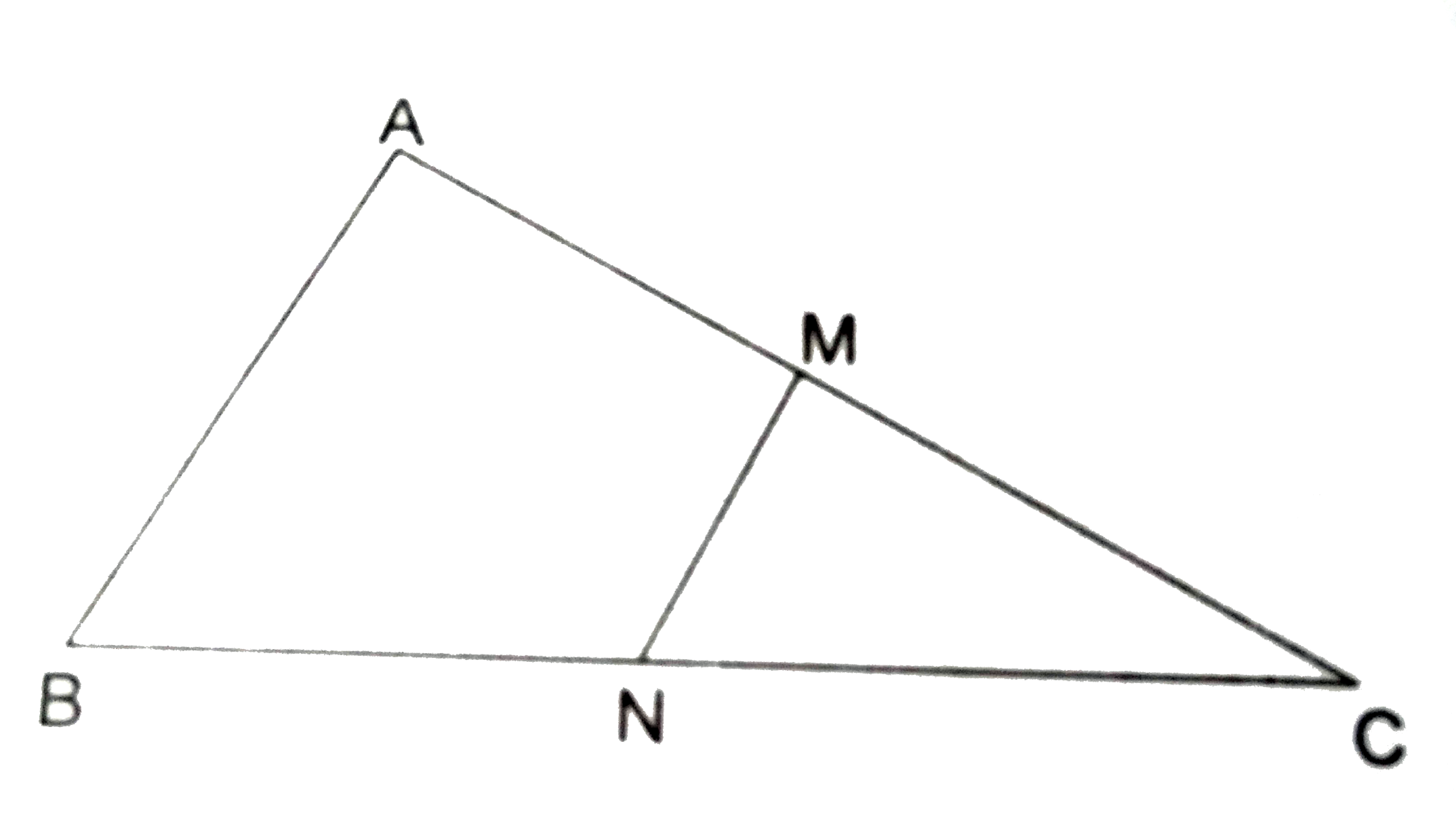
In the given figure, ∠AMN=∠MBC=76∘ . If p, q and r are the lengths of AM, MB and BC respectively then express the length of MN in term of a,b and c.
The correct Answer is:MN=aca+b
∠AMN=∠MBC⇒MN∣∣BC⇒ΔAMN~ΔABC.
∴AMAB=MNBC⇒aa+b=MNc⇒MN=aca+b
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)
53 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)
1 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D
22 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
In the given figure, AD||BC, ∠AFG=band∠BCD=c. Express b in terms of c.
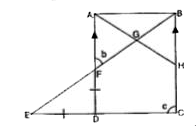 Ac2B90∘+c2C180∘−c2D90∘−c2
Ac2B90∘+c2C180∘−c2D90∘−c2In the figure below 2∠P=∠QOP, OQ and OR are bisectors of ∠Qand∠R respectively. Find ∠P
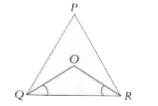 A60∘B70∘C40∘D80∘
A60∘B70∘C40∘D80∘If the pth, qth and rth terms of an A.P. are a,b,c respectively , then the value of a(q−r)+b(r−p)+c(p−q) is :
A0B1CabcDpqr
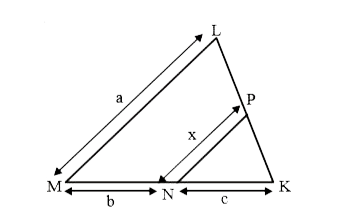
In figure, PN∣∣LM. Express x in terms of a,b and c, where a, b and c are lengths of LM, MN and NK respectively.
View SolutionIn a triangle ABC, a, b and c are the lengths of the sides and p, q and r are the lengths of its medians.
Which one of the following is correct ?
View SolutionConsider a triangle ABC, G be the centroid , AB = c, BC= a, AC = b, p,q,r are the length of the angle bisectors of A,B,C respectively and p1,p2,p3 are the length of the Altitudes from vertices A,B,C respectively: Find 1. Value of √p−21+p−22+p−23 ( Δ denotes area of triangle) is 2. The value ofGA2+GB2+GC2 is 3. The value of 1pcos(A2)+1qcos(B2)+1rcos(C2) is
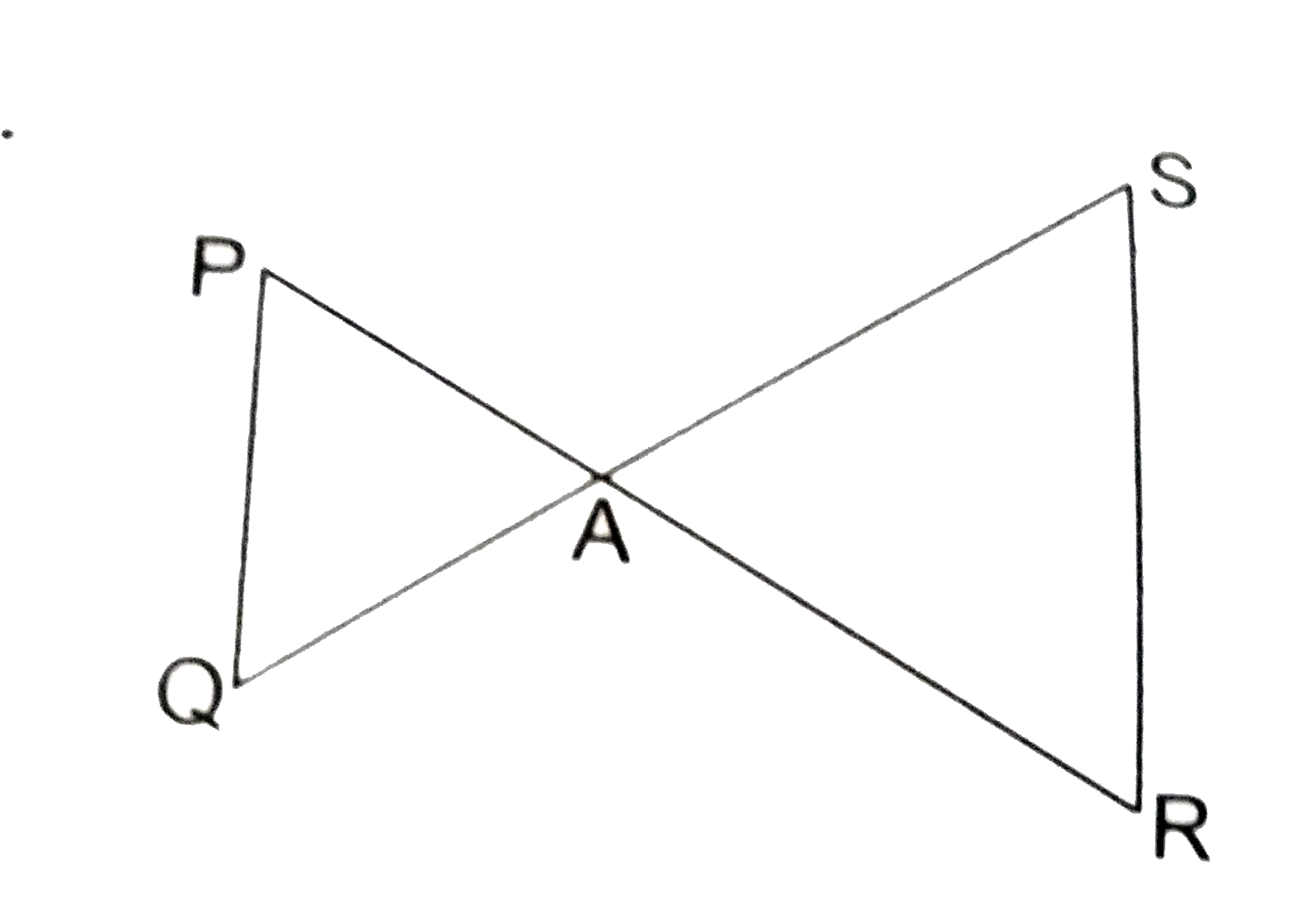
View SolutionIn the given figure, AP⋅AR=AS⋅AQ prove that ∠P=∠Sand∠Q=∠R.
View SolutionIf pth, qth and rth terms of a H.P. be respectively a, b and c then prove that (q−r)bc+(r−p)ca+(p−q)ab=0
View Solution