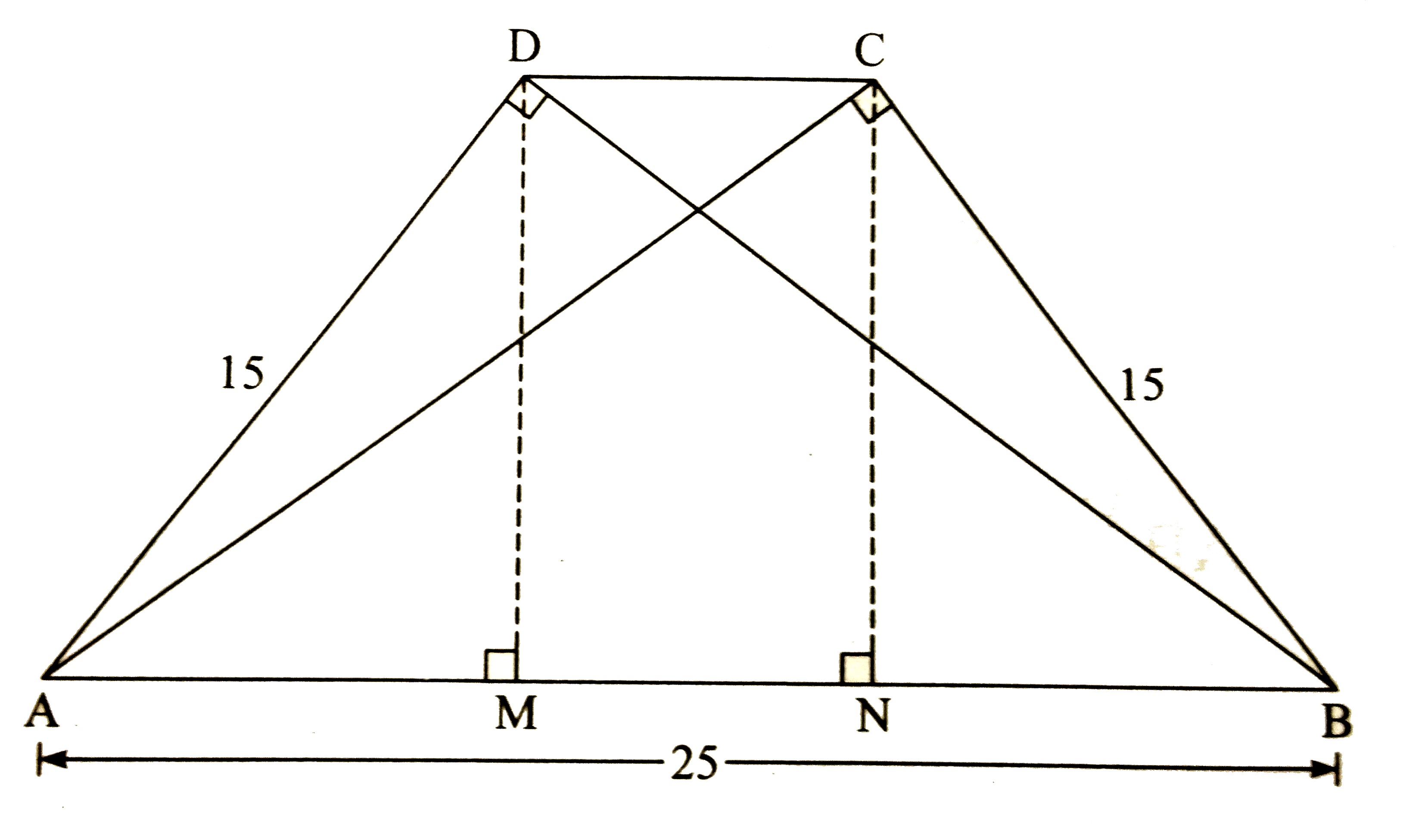
In a trapezium ABCD, seg AB∣∣ seg DC, seg BD⊥ seg AD, seg AC⊥ seg BC, if AD=15, BC=15 and AB=25. Find A(□ABCD).
Video Solution
Text Solution
The correct Answer is:∴A(□ABCD)=192sq.units
|
Answer
Step by step video, text & image solution for In a trapezium ABCD, seg AB|| seg DC, seg BD bot seg AD, seg AC bot seg BC, if AD=15, BC=15 and AB=25. Find A(square ABCD). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Problem set-29
1 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Problem set-30
1 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Problem set-27
1 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Try This
1 Videos
- QUADRATIC EQUATIONSBOOK - TARGET PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Additional problems for Practice : Based on Practice set 2.6
30 Videos
Similar Questions
Knowledge Check
In andsegBD bot sACandAD=DC then ……..
ABD2=DC×ACBBD2=AD×ACCBD2=DC×ACDnone of theseIn a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
A192cm2B232cm2C172cm2Dnone of the aboveIn a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
A192cm2B232cm2C172cm2Dnone of these
In ΔABC,segAd⊥segBC,∠C,=45∘,BD=5andAC=5√2 then find AD and BC.
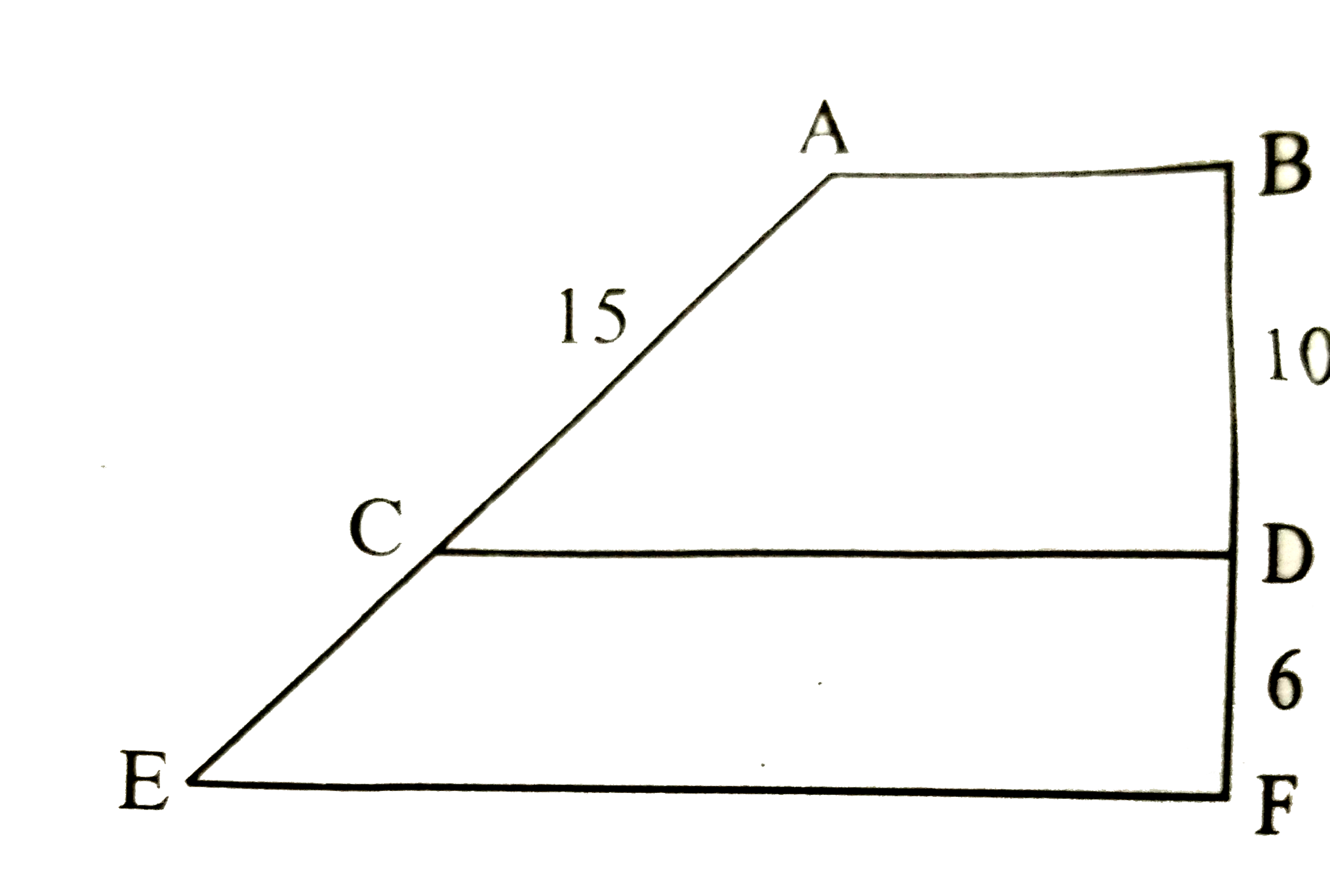
View SolutionIn the figure, seg AB∣∣ seg CD∣∣ seg EF AC=1.5, BD=10, DF=6 then AE=?
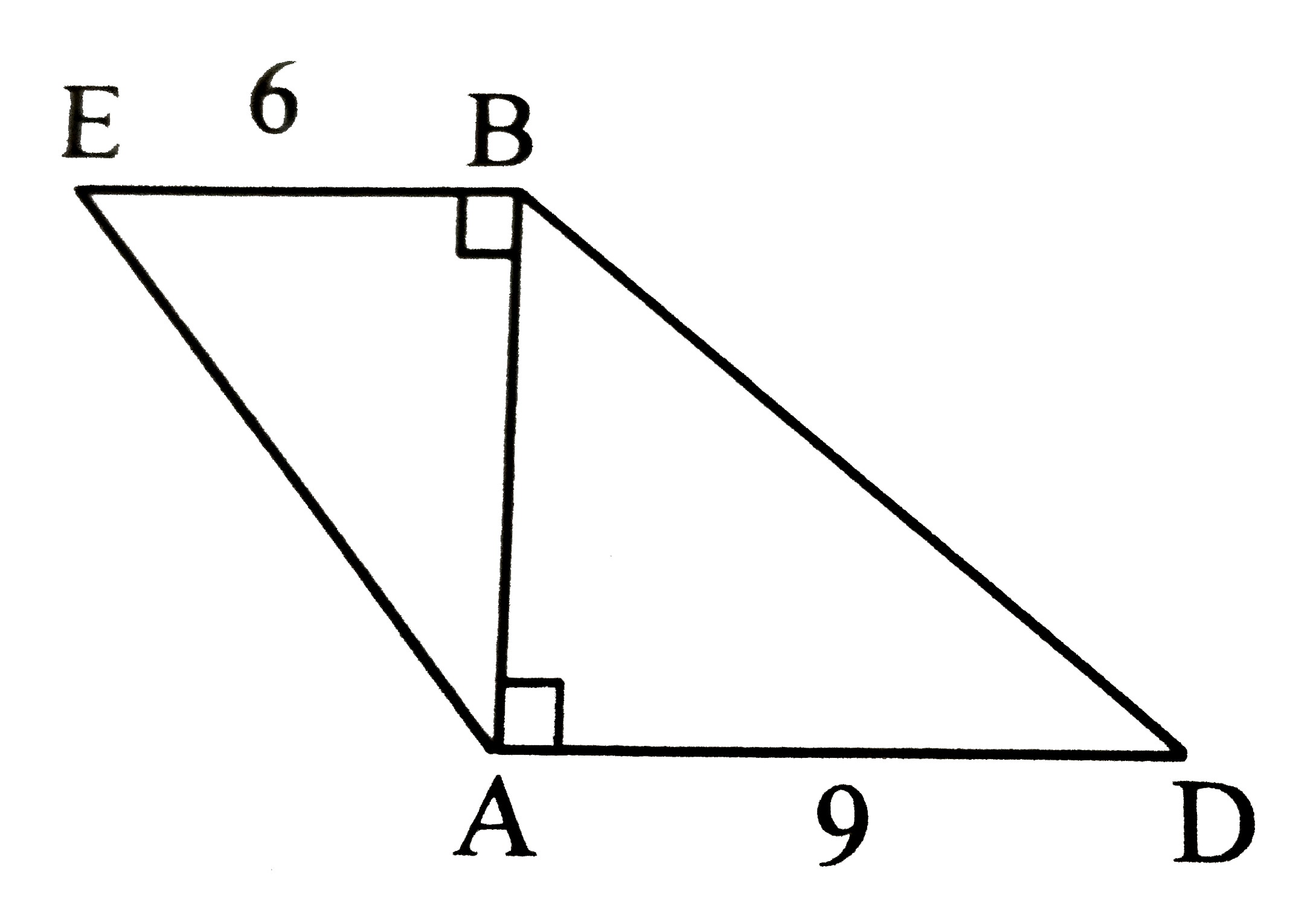
View SolutionIn the given figure, seg BE ⊥ seg AB and seg BA ⊥ seg AD. If BE = 6 and AD = 9, then find A(ΔABE)A(ΔBAD).
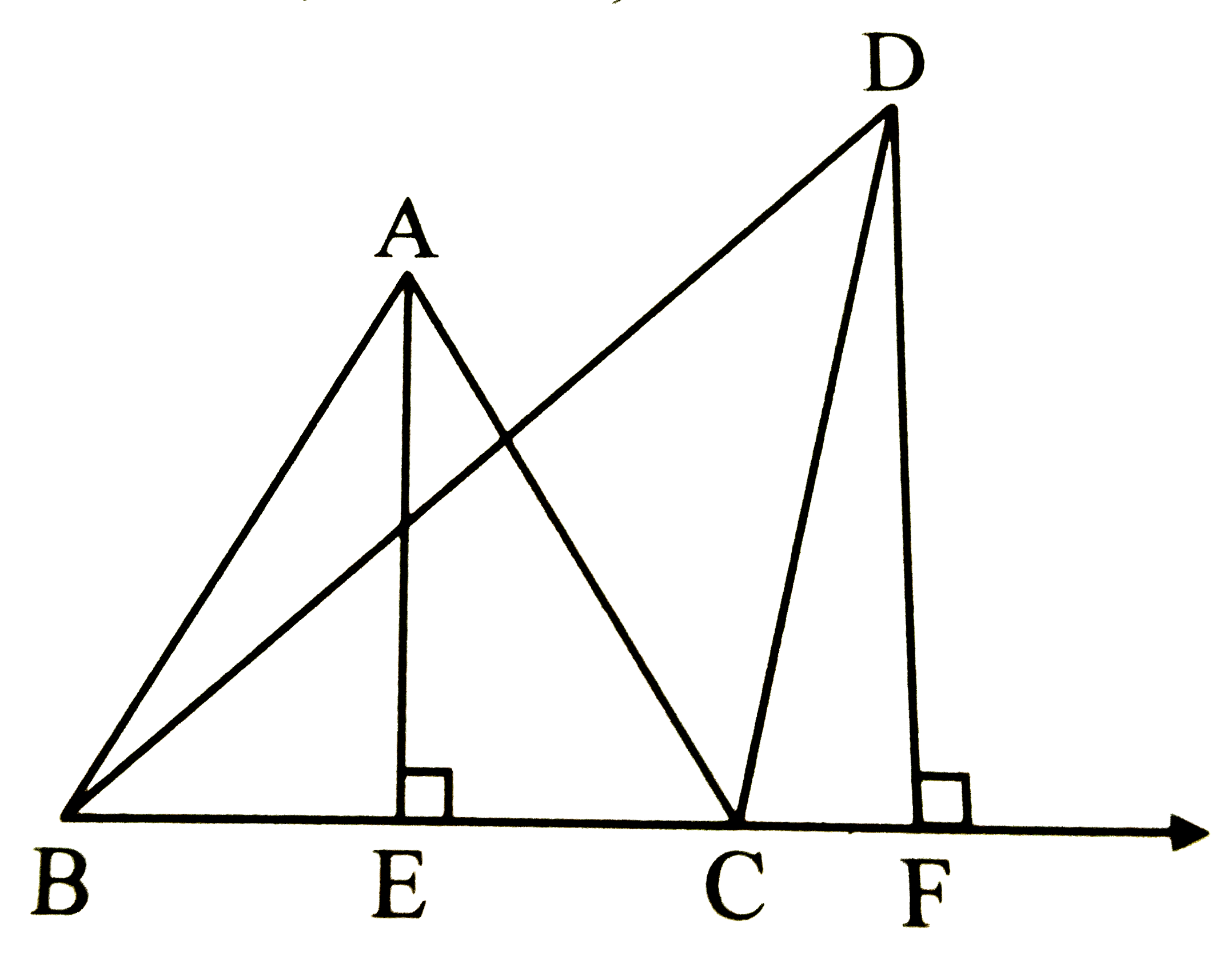
View SolutionIn given figure, seg AE ⊥ seg BC, seg DF ⊥ line BC,
AE = 4, DF = 6, then find A(ΔABC)A(ΔDBC).
View SolutionIn ΔABC,∠ACB=90∘
seg CD ⊥ seg AB
seg DE ⊥ seg CB.
Show that: CD2×AC=AD×AB×DE

View Solution

