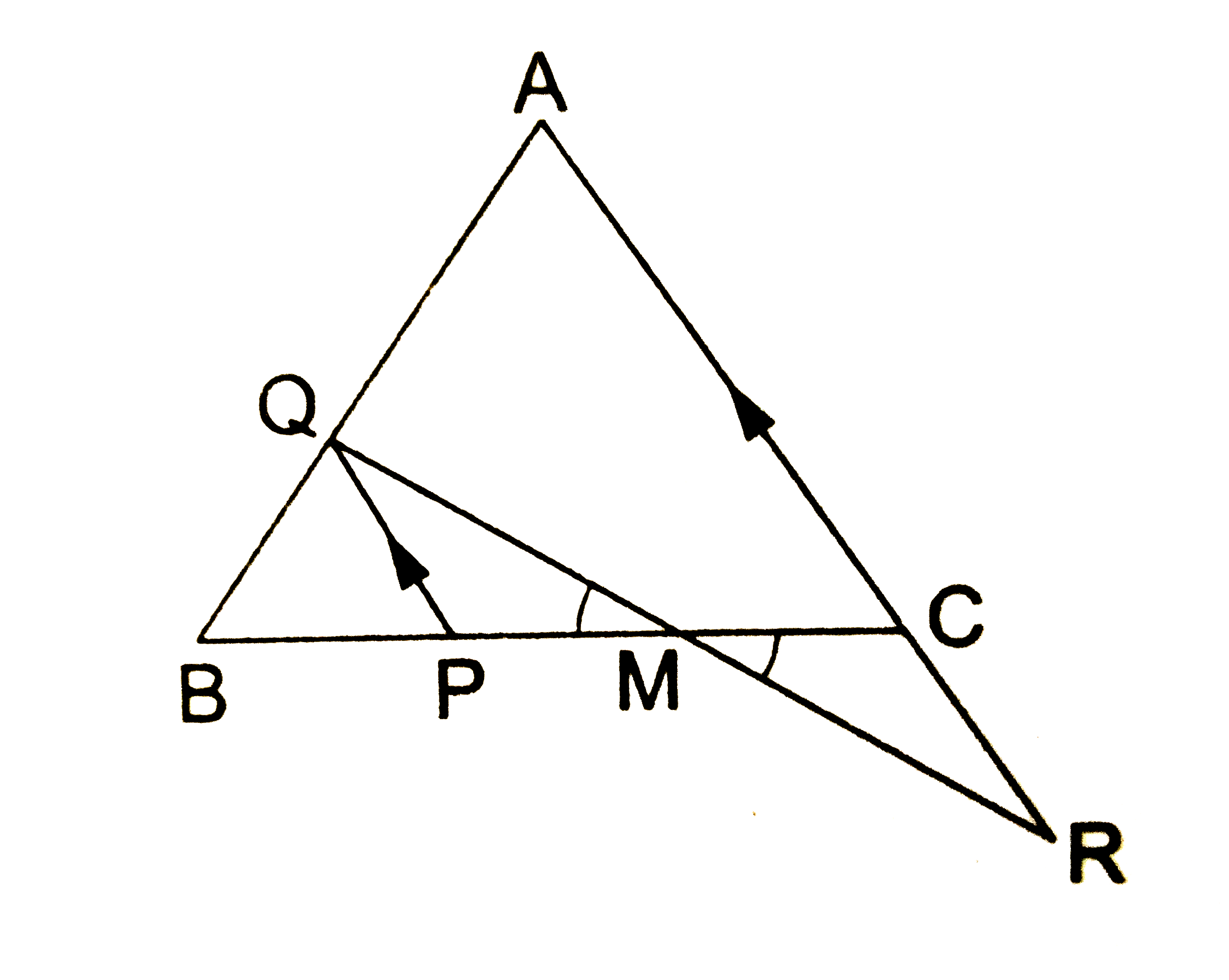
In the adjoining figure, ΔPQR is an equilateral triangle. Point S is on seg QR. such that QS=13QR. Prove that : 9PS2=7PQ2.
The correct Answer is:∴9PS2=7PQ2
Step by step video, text & image solution for In the adjoining figure, DeltaPQR is an equilateral triangle. Point S is on seg QR. such that QS=(1)/(3)QR. Prove that : 9PS^(2)=7PQ^(2). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Problem set-30
1 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Problem set-31
1 Videos
- PYTHAGORAS THEOREM BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Problem set-28
1 Videos
- PROBABILITYBOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Try This
1 Videos
- QUADRATIC EQUATIONSBOOK - TARGET PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Additional problems for Practice : Based on Practice set 2.6
30 Videos
Similar Questions
In the figure ΔPQR is an equilateral triangle. Point S is on seg QR such that
QS=13QR.
Prove that : 9PS2=7PQ2

View SolutionIn the figure 2.35,ΔPQR is an equilatral triangle. Point S is on seg QR such that QS=13QR. Prove that : 9PS2=7PQ2
View Solution1. In the figure △PQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN2=3PR2
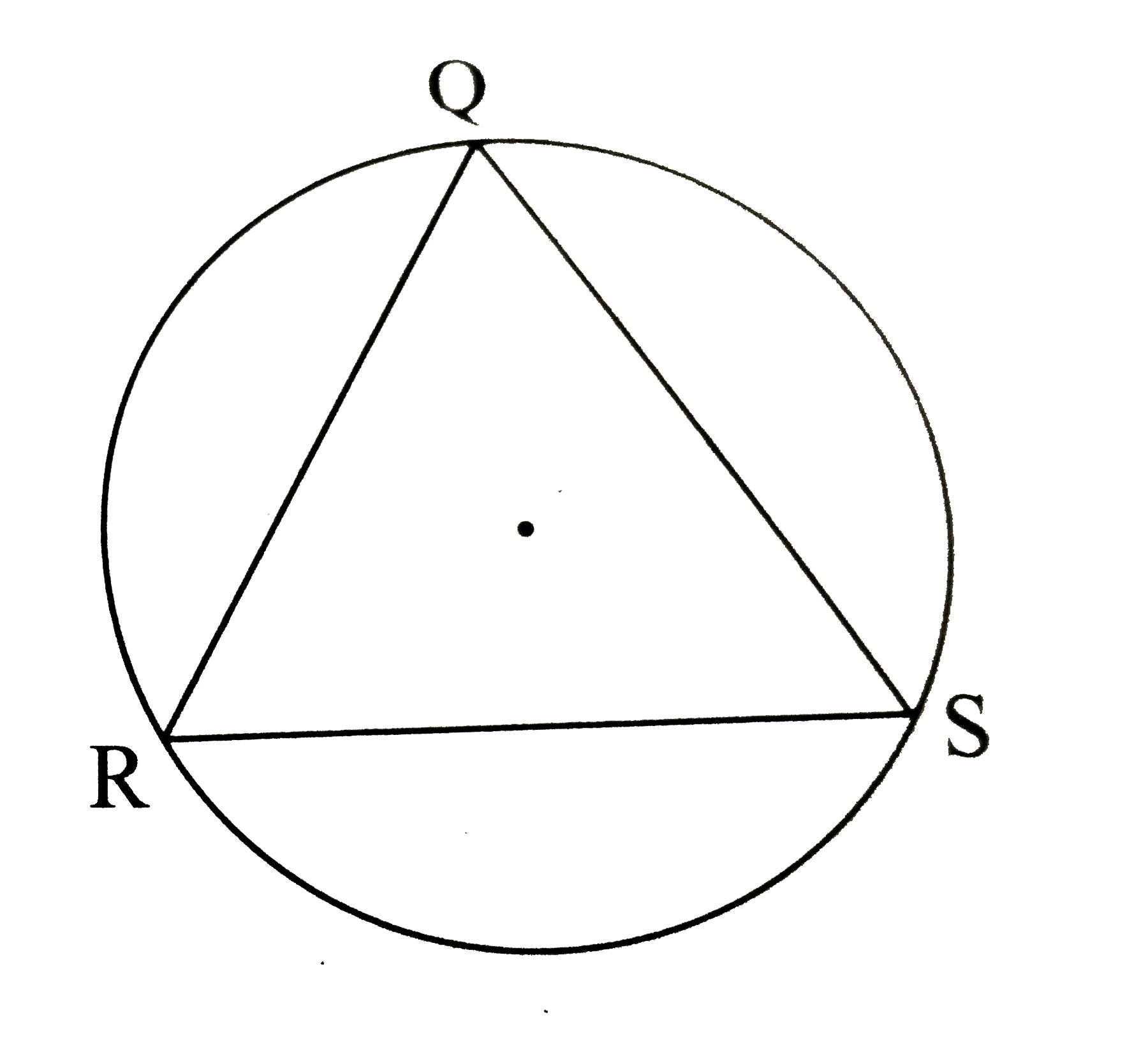
View SolutionIn the given figure, ABC is an equilateral triangle; PQ∣∣AC and AC is produced to R such that CR=BP. Prove that QR bisects PC
View SolutionIn the givne figure, ABC is an equilateral triangle, PQ||AC and AC is produced to R such that CR = BP. Prove that QR bisects PC.
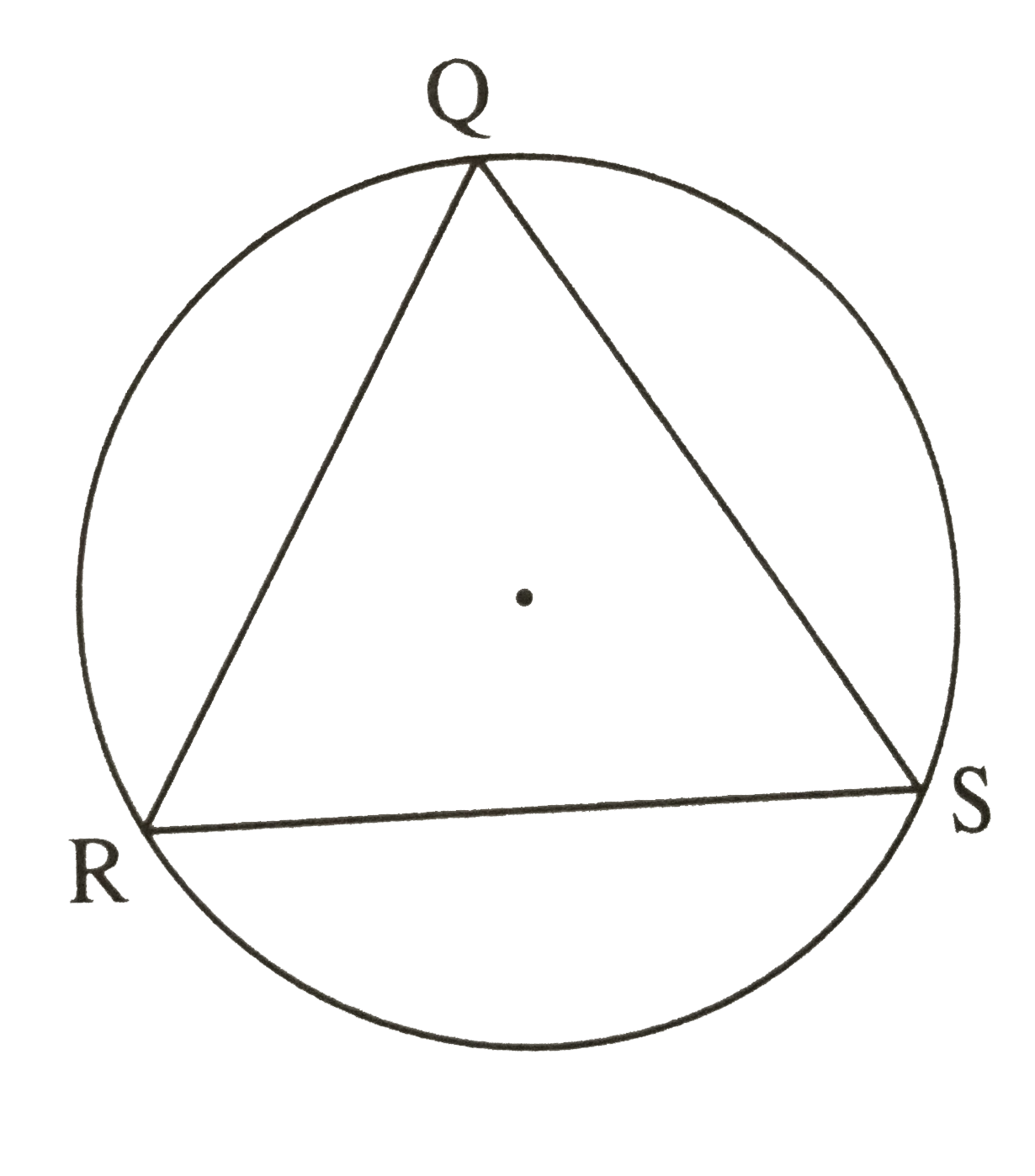
View SolutionIn the figure , ΔQRS is an equilateral triangle.
Prove that
(1) arc RS ≅arcQS≅ arc QR
(2) m (arc QRS ) =240∘.
Proof :
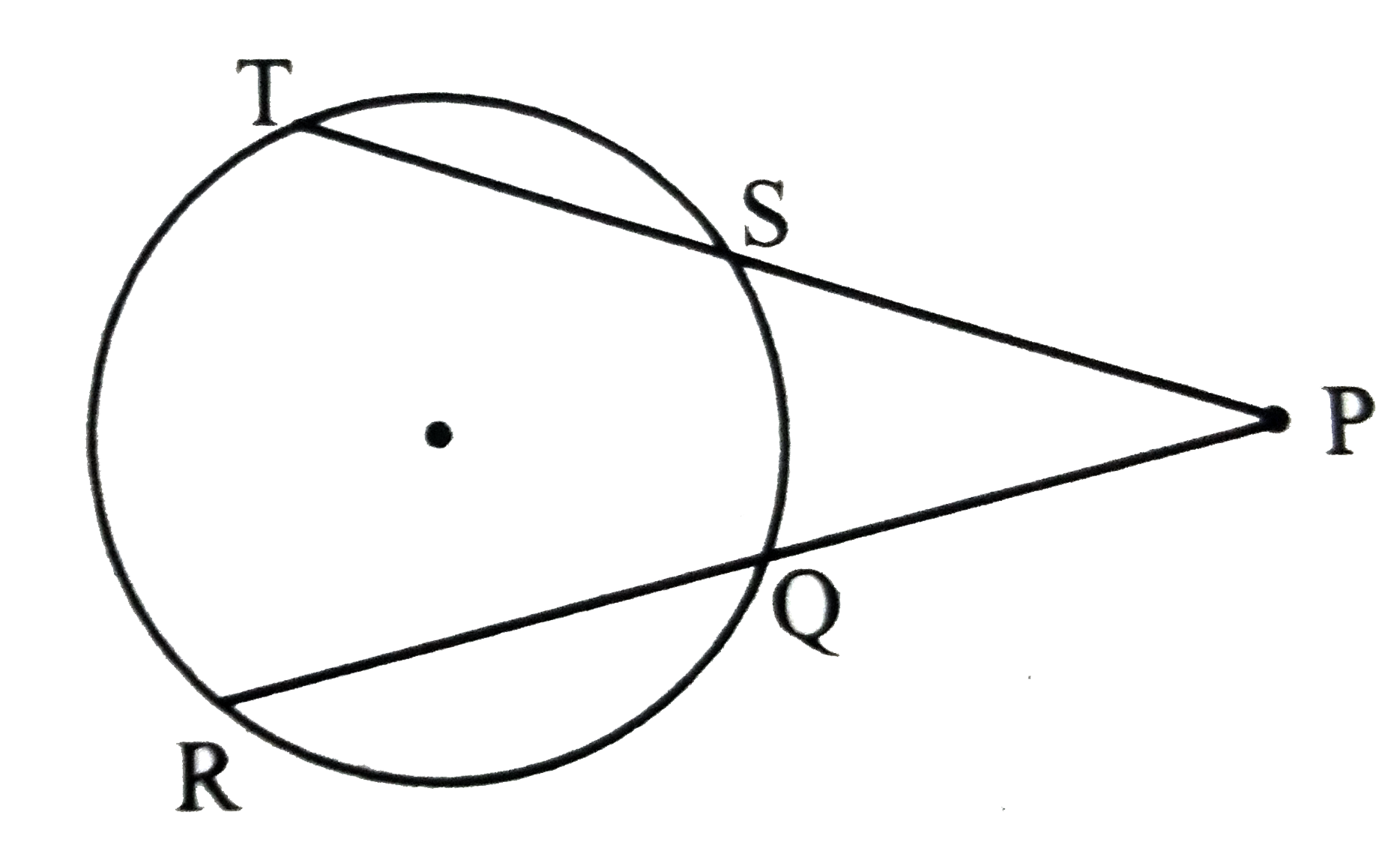
View SolutionIn the adjoining figure , if PQ=6,QR=10,PS=8 , find TS.
View SolutionIn the adjoining figure, PQR, is a right triangle, right angled at Q. X and Y are the points on PQ and QR such that PX:XQ=1:2 and QY:YR=2:1. Prove that 9(PY2+XR2)=13PR2
View SolutionIn figure, △QRS is an equilateral triangles. Prove that,
(1) arcRS≅arcQS≅arcQR
(2) m(arcQRS)=240∘.
View SolutionIn an isosceles triangle PQR, PQ =PR and S is any point on side QR. Then prove that: PQ2−PS2=QS×SR.
View Solution
