In a triangle side has equation and side has equation If the midpoint of is 5, 6), then find the equation of
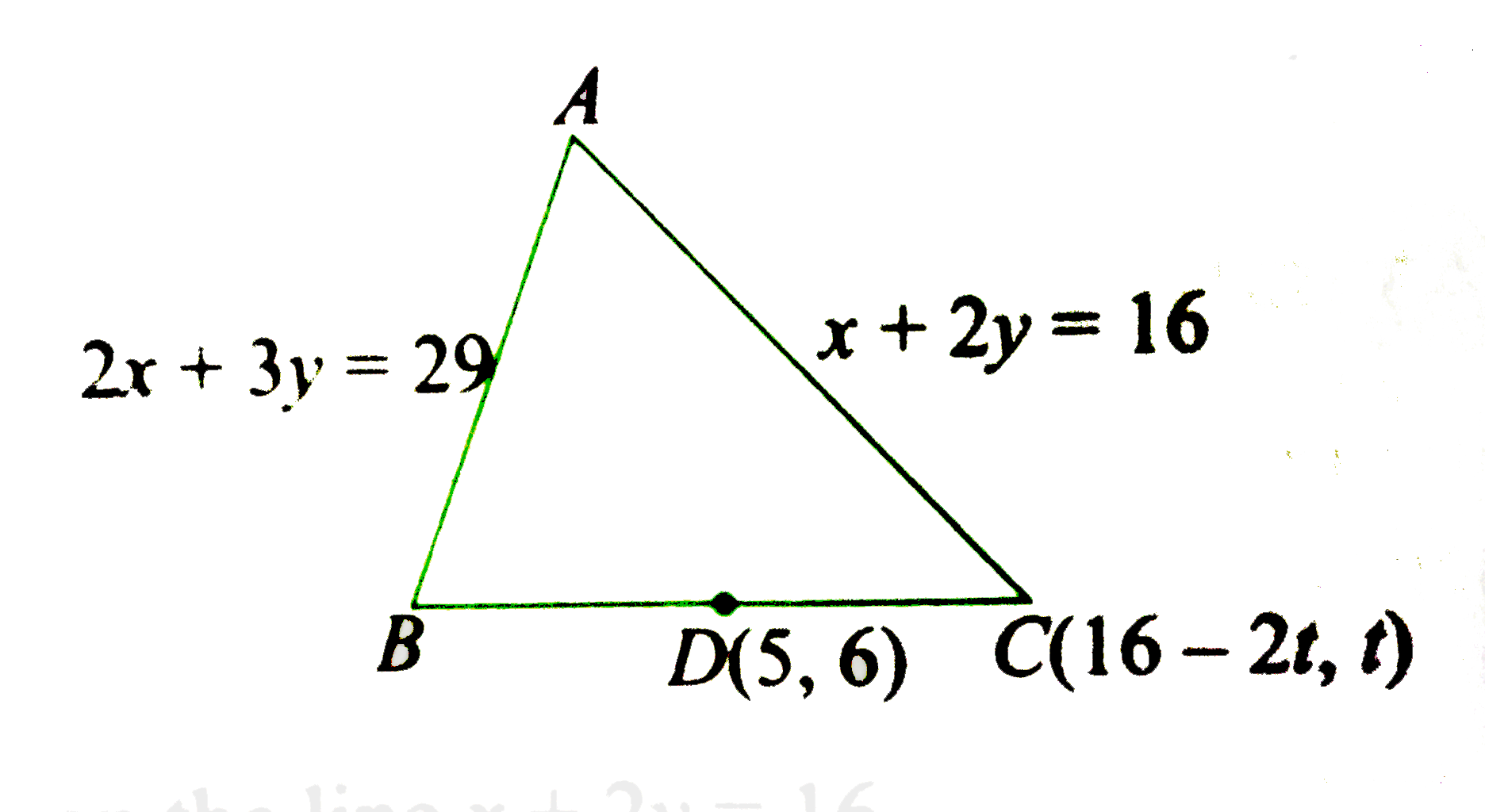
Vertex C lies on the line x+2y = 16.
So, let point C be (16-2t,t).
D(5,6) is midpoint of BC.
So, point B is (2t-6, 12-t)
Point B lies on the line 2x+3y-29 = 0
Hence, point B is (4,7)
Therefore, equation of line BC is
or x+y = 11
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
In a triangle ABC, side AB has equation 2x+3y=29 and side AC has equation x+2y=16. If the midpoint of BC is 5, 6), then find the equation of BC.
View SolutionThe sides ABandAC of a triangle ABC are respectively 2x+3y=29andx+2y=16 respectively. If the mid-point of BCis(5,6) then find the equation of BC.
View SolutionThe sides AB and AC of a triangle ABC are respectively 2x+3y=29 and x+2y=16 respectively. If the mid-point of BCis(5,6) then find the equation of BC
View SolutionThe sides ABandAC of a triangle ABC are respectively 2x+3y=29andx+2y=16 respectively. If the mid-point of BCis(5,6) then find the equation of BC.
View SolutionIn triangle ABC , the equation of the right bisectors of the sides AB and AC are x+y=0 and y−x=0 , respectively. If A≡(5,7) , then find the equation of side BC.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionThe equations of the perpendicular bisectors of the sides ABandAC of triangle ABC are x−y+5=0 and x+2y=0 , respectively. If the point A is (1,−2) , then find the equation of the line BC.
View SolutionIn triangle ABC , the equation of side BC is x−y=0. The circumcenter and orthocentre of triangle are (2, 3) and (5, 8), respectively. The equation of the circumcirle of the triangle is a) x2+y2−4x+6y−27=0 b) x2+y2−4x−6y−27=0 c) x2+y2+4x−6y−27=0 d) x2+y2+4x+6y−27=0
View SolutionA vertex of an equileteral triangle is (2;3) and the equation of the opposite sides is x+y=2 .Find the equation of the other sides of triangle .
View SolutionA triangle has two sides y=m1x and y=m2x where m1 and m2 are the roots of the equation bα2+2hα+a=0. If (a,b) be the orthocenter of the triangle, then find the equation of the third side in terms of a, b and h.
View Solution
