In a triangle ABC, the measure of angle A is 40° less than the measure of angle B and 50° less than that of angle C. Find the measure of ∠A.
To solve the problem, we need to find the measure of angle A in triangle ABC given the relationships between the angles.
1. Define the angles:
Let the measure of angle A be x.
2. Express angles B and C in terms of angle A:
According to the problem:
- Angle A is 40° less than angle B:
B=x+40°
- Angle A is 50° less than angle C:
C=x+50°
3. Use the triangle angle sum property:
The sum of the angles in a triangle is always 180°:
A+B+C=180°
Substituting the expressions for B and C:
x+(x+40°)+(x+50°)=180°
4. Combine like terms:
Simplifying the equation:
x+x+40°+x+50°=180°
3x+90°=180°
5. Isolate x:
Subtract 90° from both sides:
3x=180°−90°
3x=90°
6. Solve for x:
Divide both sides by 3:
x=90°3=30°
7. Conclusion:
The measure of angle A is 30°.
Final Answer:
The measure of angle A is 30°.
---
Let the measure of angle A be x.
According to the problem:
- Angle A is 40° less than angle B:
B=x+40°
- Angle A is 50° less than angle C:
C=x+50°
The sum of the angles in a triangle is always 180°:
A+B+C=180°
Substituting the expressions for B and C:
x+(x+40°)+(x+50°)=180°
Simplifying the equation:
x+x+40°+x+50°=180°
3x+90°=180°
Subtract 90° from both sides:
3x=180°−90°
3x=90°
Divide both sides by 3:
x=90°3=30°
The measure of angle A is 30°.
The measure of angle A is 30°.
Topper's Solved these Questions
Similar Questions
In triangle XYZ, the measure of angle X is 30° greater than the measure of angle Y and angle Z is a right angle. Find the measure of∠Y.
View SolutionThe given figure shows an isosceles triangle ABC with AB = BC and angle B = 20∘. Points D&E are on AB & BC respectively so that the measure of angle CAE is 40∘ degrees and the measure of angle ACD is 50∘ degrees. DE and AC meet at F. Find the measure of angle AFD.
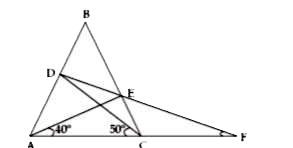
View Solution
Knowledge Check
In a triangle ABC, if AB = BC and the measure of angle C is 75∘, then the measure of angle B is:
A30∘B60∘C75∘D52.5∘In a rhombus ABCD, measure of angle CAB is25∘. What is the measure of angle ABC?
A65∘B50∘C40∘D130∘Angles A and B are complementary and the measure of angle A is twice the measure of angle B. Find the measures of angles A and B
A∠A=20∘,∠B=40∘B∠A=30∘,∠B=60∘C∠A=60∘,∠B=30∘D∠A=15∘,∠B=30∘
Find the measure of an angle which is 30∘ less than its supplement.
View SolutionIn a triangle ABC the angle B is greater than angle C. If the measure of angles B and C satisfy the equation 4sin3x−3sinx+0.75=0 then the measure of angle A is (A) π2 (B) 2p3 (C) π6 (D) 5π6
View SolutionFind the measure of an angle which is 35∘ less than its supplement.
View SolutionIn ΔABC,(a+b)(a−b)=c(b+c) then measure of angle A is
View SolutionFind the measure of an angle which is 32∘ less than its supplement.
View Solution
