In an equilateral triangle ABC, If AD⊥BC, B-D-C and AB = 12 cm, then the value of AD is
6 cm
6√3cm
4 cm
4√3cm
Step by step video & image solution for In an equilateral triangle ABC, If ADbotBC, B-D-C and AB = 12 cm, then the value of AD is by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Aditional Problems for Practice(Based on the Practice Set 2.1)23videos
PYTHAGORAS THEOREM
- BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Aditional Problems for Practice(Based on the Practice Set 2.2)5videos
PYTHAGORAS THEOREM
- BOOK - TARGET PUBLICATIONCHAPTER - PYTHAGORAS THEOREM EXERCISE - Activities for Practice2videos
PYTHAGORAS THEOREM
- BOOK - TARGET PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Try This1videos
PROBABILITY
- BOOK - TARGET PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - Additional problems for Practice : Based on Practice set 2.630videos
QUADRATIC EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
In an equilateral ΔABCif AD⊥BC, then
A2AB2=3AD2B3AB2=4AD2C5AB2=6AD2D4AB2=5AD2 - Question 2 - Select One
In an equilateral triangle ABC, the side BC is trisected at D. Find the value of AD2 :
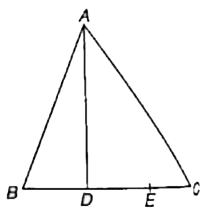 A97AB2B79AB2C34AB2D45AB2
A97AB2B79AB2C34AB2D45AB2 - Question 3 - Select One
ΔABC is equilateral triangle. Where AD = DE = BE, D and E lies on the AB. If each side of the triangle be 6cm. Then the area of shaded region.
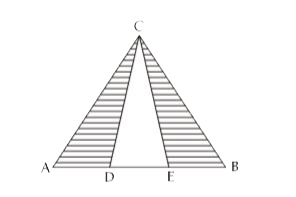 A9cm2B6√3cm2C5√3cm2Dnone of the above
A9cm2B6√3cm2C5√3cm2Dnone of the above
In a triangle ABC, ∠BCA=90∘ and CD is perpendicular to AB. If AD = 4 cm and BD = 9 cm, then the value of DC will be
View SolutionIs 7×6×5×4×3×2×1+5 composite number ? Justify your answer.
View SolutionThe side AB of an equilateral triangle ABC is produced to D such that BD=2AC the value of CD2AB2 is
View SolutionIn the equilateral triangle ABC, AD = DE = BE, D and E lies on the AB. If each side of the triangle (i.e., AB, BC and AC) be 6 cm, then the area of the shaded region is:
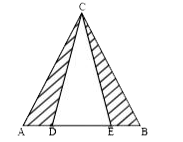 View Solution
View SolutionIn △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
View Solution

