In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.

Video Solution

Text Solution

Verified by Experts

Let AB=BC=CA=a
In $△ A D B and △ A D C$ .
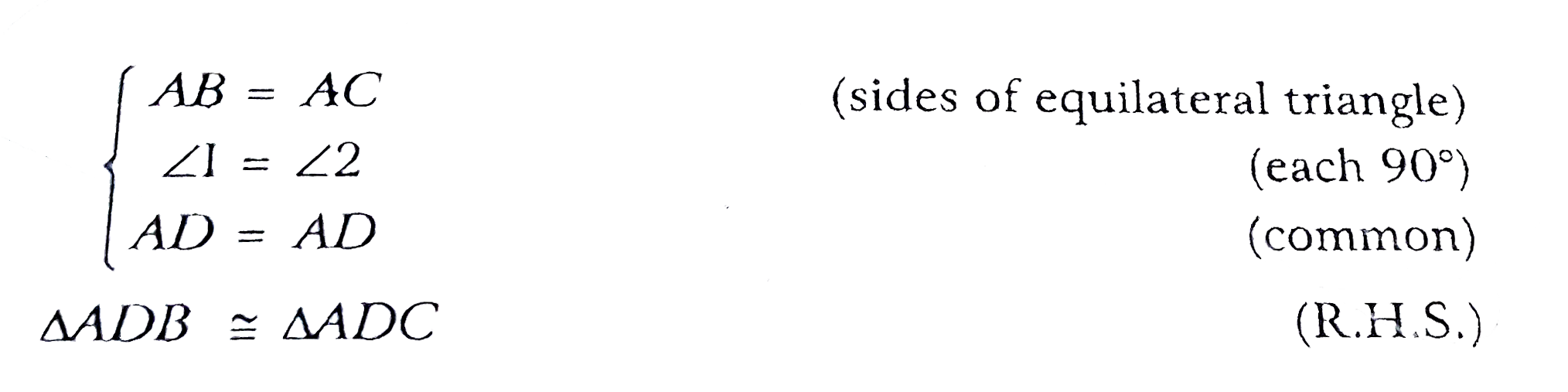(common) ,
$△ A D B ≅ △ A D C$ ( R.H.S)
$B D = D C = \frac{B C}{2} = \frac{a}{2}$
Now in $△ A D B$ by pythagoras theorem
$A B^{2} = A D^{2} + B D^{2}$
$a^{2} = A D^{2} + {(\frac{a}{2})}^{2}$
$A D^{2} = a^{2} - \frac{a^{2}}{4} \Rightarrow A D^{2} = \frac{3 a^{2}}{4}$
$4 A D^{2} = 3 a^{2} \Rightarrow 4 A D^{2} = 3 A B^{2}$
Hence , 3 times the square of side is equal to 4 times the square of altitude.

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In an equilateral triangle of side 2a, calculate the length of its altitude.
A $2 a \sqrt{3}$
B $a \sqrt{3}$
C $a \frac{\sqrt{3}}{2}$
Dnone of these

NAGEEN PRAKASHAN-TRIANGLES -Revision Exercise Long Questions

Home
Ask Doubt
Profile