In an equilateral triangle with side $a$ , prove that (i) Altitude $= \frac{a \sqrt{3}}{2}$ (ii) Area $= \frac{\sqrt{3}}{4} a^{2}$

Video Solution

Text Solution

Verified by Experts

LEt $Δ A B C$ be an equilateral triangle with side a.
Then, $A B = A C = B C = a$
Draw $A D ⊥ B C$ .
In $Δ A D B and Δ A D C$ , we have
$A B = A C (given), ∠ B = ∠ C = 60^{\circ}$
and $∠ A D B = ∠ A D C = 90^{\circ}$
$∴ Δ A D B ≅ Δ A D C$ .
$∴ B D = D C = \frac{a}{2}$

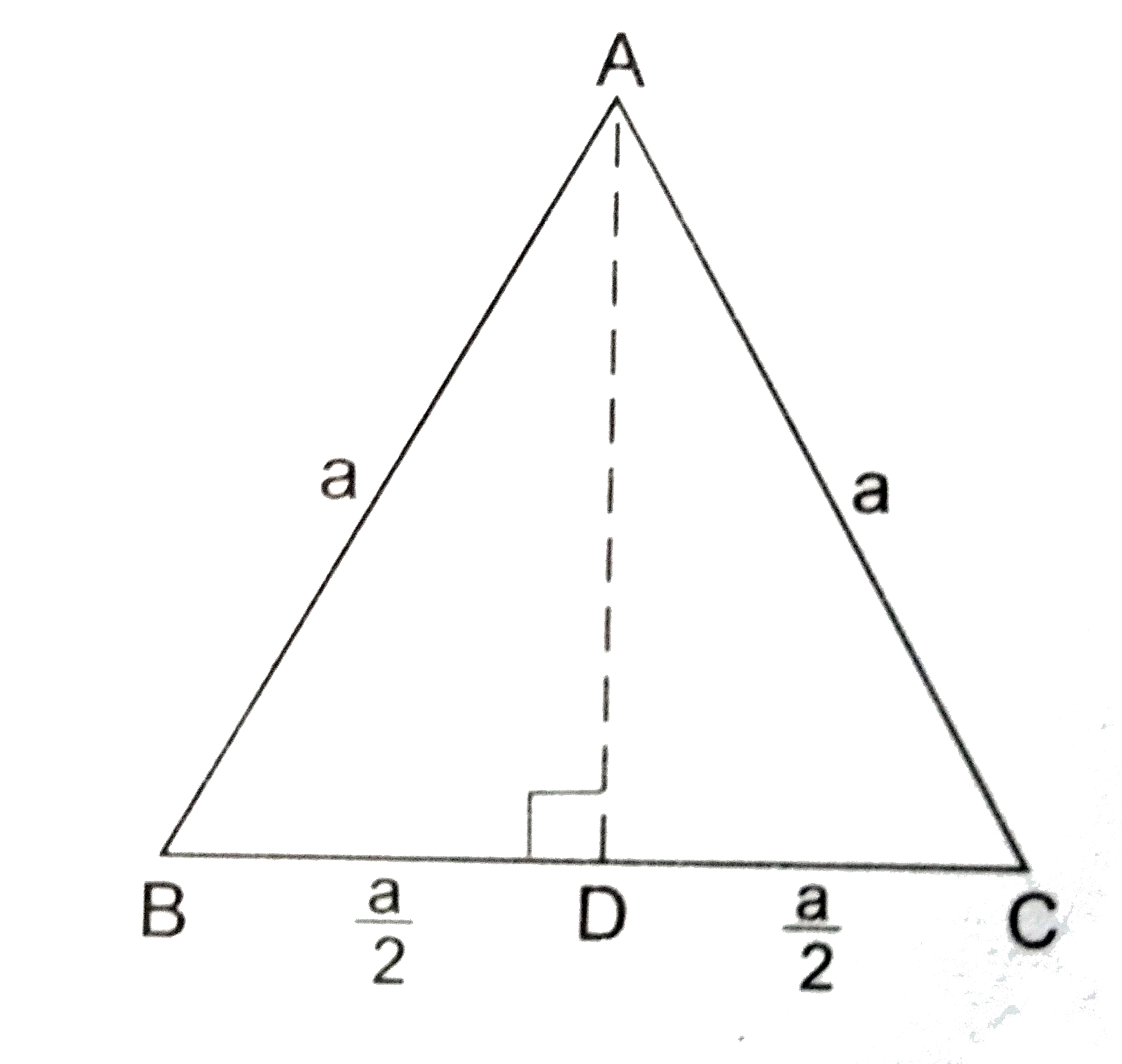
(i) From rigth $Δ A D B$ , we have
$A B^{2} = A D^{2} + B D^{2}$ [ by Pythagora's theorem]
$\Rightarrow A D = \sqrt{A B^{2} - B D^{2}}$
$= \sqrt{a^{2} - (\frac{a}{2^{2}})} = \sqrt{a^{2} - \frac{a^{2}}{4}} = \sqrt{\frac{3 a^{2}}{4}} = \frac{\sqrt{3}}{2} a$ .
Hence, altitude $= \frac{\sqrt{3}}{2} a$
(ii) Area of $Δ A B C = \frac{1}{2} \times base \times altitude = (\frac{1}{2} \times B C \times A D)$
$= (\frac{1}{2} \times a \times \frac{\sqrt{3}}{2} a)$ [ using(i)[
$= (\frac{\sqrt{3}}{4} a^{2})$ sq units.
Hence , area $(Δ A B C) = (\frac{\sqrt{3}}{4} a^{2})$ sq units

Updated on:21/07/2023