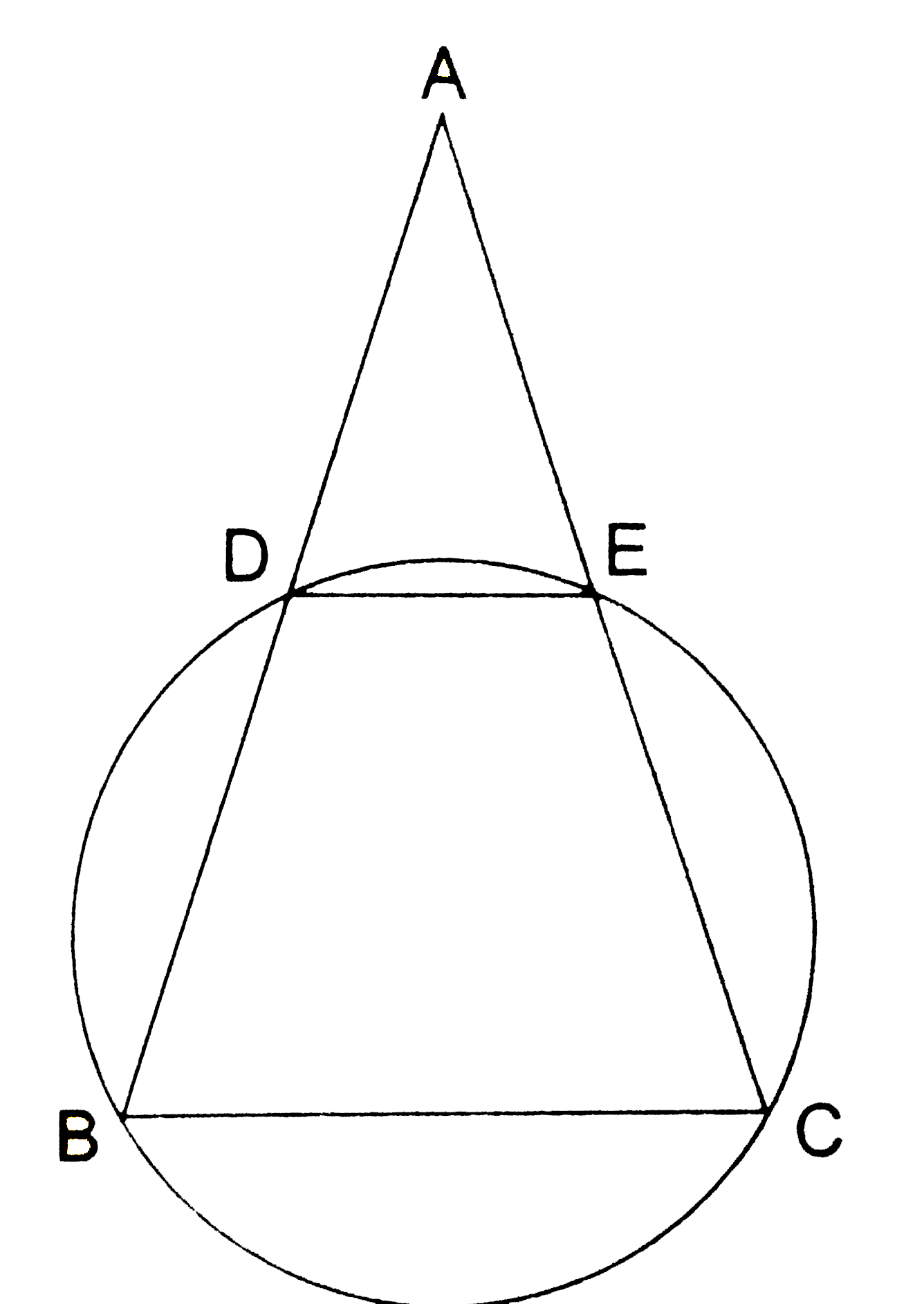
In an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides AB and AC at D and E respectively. Prove that DEBC
AB= AC
⇒∠ABC=∠ACB ….(i)
Side BD of the cyclic quadrilateral BCED is produced to A.
∴∠ADE=∠ACB …(ii)
[ext. ∠ADE=int. opp. ∠C] .
From (i) and (ii) , we get
∠ABC=∠ADE.
But, these are corresponding angles.
Hence,DE∣∣BC
Similar Questions
In an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides ABandAC atDandE respectively. Prove that DECB.
View SolutionIn an isosceles triangle ABC with AB=AC, a circle passing through B and C intersects the sides AB and AC at D and E respectively. Prove that DEBC
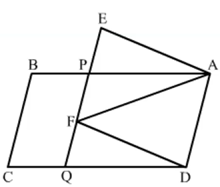
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
View SolutionLet ABC be an isosceles triangle with AB=AC and let D, E, F be the mid points of BC, CA and AB respectively. Show that AD⊥FE and AD is bisected by FE
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionLet ABC be an isosceles triangle in which AB=AC If D,E,F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
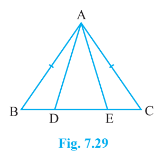
View SolutionIn an isosceles triangle ABC with AB=AC, D and E are points on BCsuch that BE=CD(see Fig. 7.29). Show that AD=AE
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
View SolutionIn Figure, triangle ABC is right-angled at B. Give that AB=9CM, AC=15CM,andD,E are the mid-points of the sides ABandAC respectively, calculate
The length of BC
(ii) The area of ADE
View Solution
