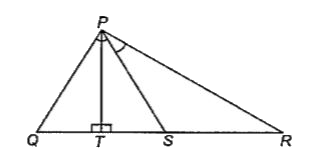
In and PO is the bisector of . If and then in degrees
The correct Answer is:a
To solve the problem, we need to find the angle ∠DPO in triangle PQR given that PD⊥QR and PO is the bisector of ∠QPR. We are also given the angles ∠PQR=65∘ and ∠PRQ=23.5∘.
1. Identify the Angles:
We know:
∠PQR=65∘
∠PRQ=23.5∘
2. Find ∠QPR:
Using the fact that the sum of angles in a triangle is 180∘:
∠QPR=180∘−∠PQR−∠PRQ
Substituting the known values:
∠QPR=180∘−65∘−23.5∘=180∘−88.5∘=91.5∘
3. Determine ∠QPO and ∠OPR:
Since PO is the bisector of ∠QPR:
∠QPO=∠OPR=12∠QPR=12×91.5∘=45.75∘
4. Find ∠QPD:
Since PD⊥QR, we can find ∠QPD:
∠QPD=180∘−∠PQR−90∘
Substituting the known values:
∠QPD=180∘−65∘−90∘=25∘
5. Calculate ∠DPO:
Now we can find ∠DPO using:
∠DPO=∠QPO−∠QPD
Substituting the values we found:
∠DPO=45.75∘−25∘=20.75∘
Thus, the value of ∠DPO is 20.75∘.
Final Answer:
∠DPO=20.75∘
We know:
∠PQR=65∘
∠PRQ=23.5∘
Using the fact that the sum of angles in a triangle is 180∘:
∠QPR=180∘−∠PQR−∠PRQ
Substituting the known values:
∠QPR=180∘−65∘−23.5∘=180∘−88.5∘=91.5∘
Since PO is the bisector of ∠QPR:
∠QPO=∠OPR=12∠QPR=12×91.5∘=45.75∘
Since PD⊥QR, we can find ∠QPD:
∠QPD=180∘−∠PQR−90∘
Substituting the known values:
∠QPD=180∘−65∘−90∘=25∘
Now we can find ∠DPO using:
∠DPO=∠QPO−∠QPD
Substituting the values we found:
∠DPO=45.75∘−25∘=20.75∘
∠DPO=20.75∘
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS ( VERY SHORT ANSWER TYPE QUESTIONS)
28 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - TEST YOUR CONCEPTS ( SHORT ANSWER TYPE QUESTIONS)
15 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level 2
20 Videos
- FormulaeBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FormulaeEXERCISE - Level 3
7 Videos
- INDICESBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICESEXERCISE - CONCEPT APPLICATION (Level 3)
7 Videos
Similar Questions
Knowledge Check
In triangle ABC, AD⊥BC and AO is the bisector of ∠BAC. If ∠ABC=65∘and∠ACB=231∘2 , then ∠DAO is ____ (in degrees)
A201∘4B201∘5C201∘2D203∘4In ΔPQR,PQ=3 and QR=7 Then ……….holds good.
APR=4BPR=10C10>PR>4D7>PR>3In ΔPQR, Ps is the bisector of <P and PT⊥QR, then <TPS is equal to
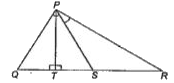 A<Q+<RB90∘+12<QC90∘−12<RD12(<Q−<R)
A<Q+<RB90∘+12<QC90∘−12<RD12(<Q−<R)
In the figure, ray QS is the bisector of ∠PQR and PQ=QR.
Then PSSR=………..
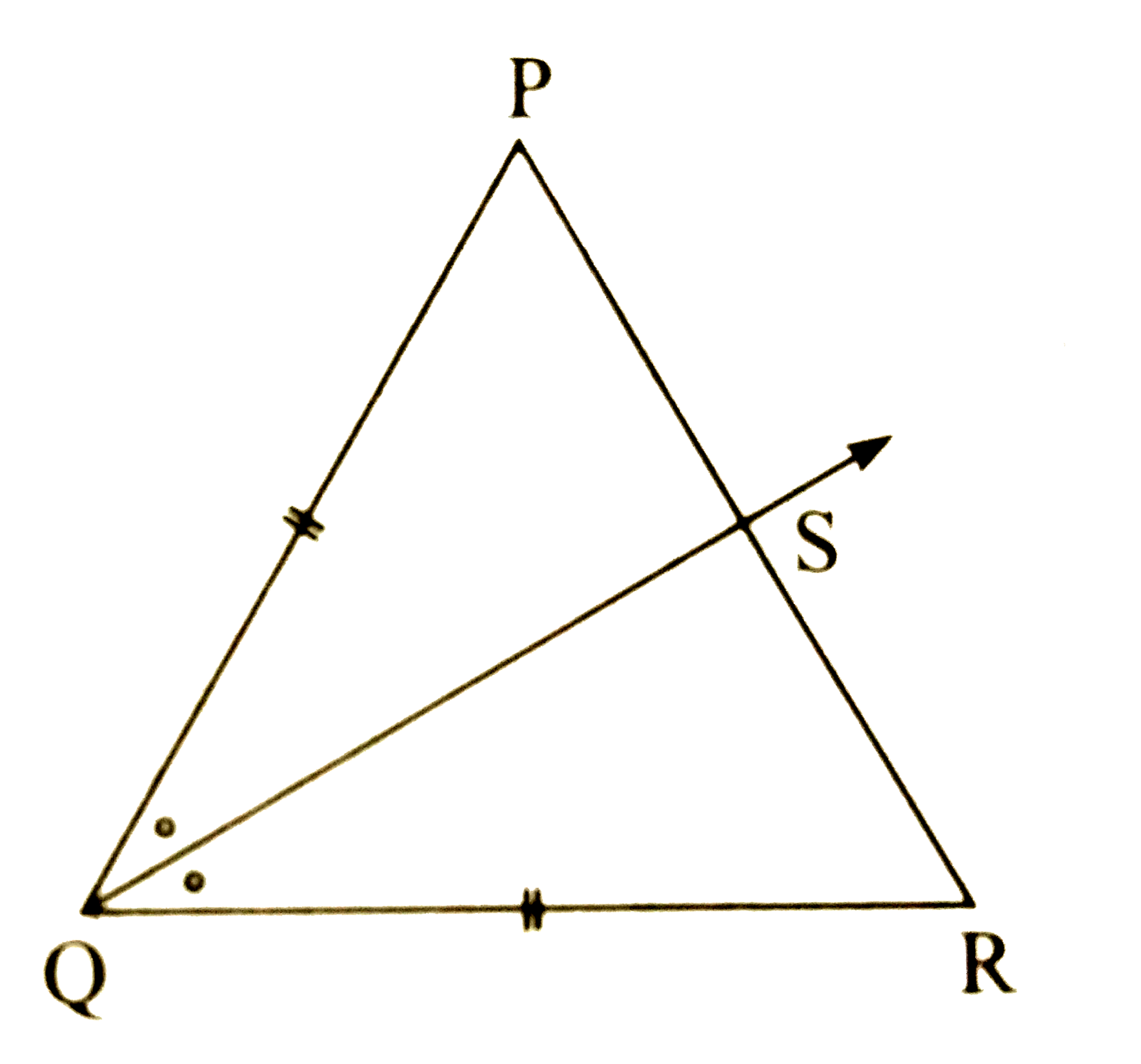
View SolutionIn Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
View SolutionIn cyclic quadrilateral PQRS, ∠SQR=60∘ and ∠QPR=20∘. Then, ∠QRS=
View SolutionIn a triangle PQR, PQ=20 cm and PR =6 cm, the side QR is :
View SolutionPQRS is a cyclic uadrilateral such that PR is the diameter of the circle. If ∠QPR=50∘ and ∠SPR=60∘, then ∠QRS=…….
View Solution