In ΔPQR,Q is a right angle, PQ = 3 and QR = 4. If ∠P=αandR=β, then tan β is equal to
43
34
35
53
The correct Answer is:B
To solve the problem, we need to determine the value of tanβ in triangle PQR, where Q is the right angle, PQ=3, and QR=4.
1. Identify the Triangle and its Sides:
- We have triangle PQR with Q as the right angle.
- The sides are given as PQ=3 (the side opposite angle R) and QR=4 (the side opposite angle P).
2. Determine the Relationship for tanβ:
- In a right triangle, the tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side.
- For angle R (which is β), the opposite side is PQ and the adjacent side is QR.
3. Write the Formula for tanβ:
tanβ=OppositeAdjacent=PQQR
4. Substitute the Values:
- We know PQ=3 and QR=4.
tanβ=34
5. Final Result:
- Therefore, tanβ=34.
- We have triangle PQR with Q as the right angle.
- The sides are given as PQ=3 (the side opposite angle R) and QR=4 (the side opposite angle P).
2. Determine the Relationship for tanβ:
- In a right triangle, the tangent of an angle is defined as the ratio of the length of the opposite side to the length of the adjacent side.
- For angle R (which is β), the opposite side is PQ and the adjacent side is QR.
tanβ=OppositeAdjacent=PQQR
- We know PQ=3 and QR=4.
tanβ=34
- Therefore, tanβ=34.
Topper's Solved these Questions
- TRIGONOMETRIC RATIOSBOOK - ARIHANT PUBLICATION BIHARCHAPTER - TRIGONOMETRIC RATIOSEXERCISE - EXAM BOOSTER (FOR CRACKING EXAM)
25 Videos
- TRIGONOMETRIC IDENTITIESBOOK - ARIHANT PUBLICATION BIHARCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - EXAM BOOSTER (FOR CRACKING EXAM)
35 Videos
- VOLUME AND SURFACE AREA BOOK - ARIHANT PUBLICATION BIHARCHAPTER - VOLUME AND SURFACE AREA EXERCISE - Exam Booster For Cracking Exam
42 Videos
Similar Questions
Knowledge Check
In ΔPQR, If ∠R>∠Q, then
AQR>PRBPQ>PRCPQ<PRDQR>PRIn ΔPQR,PQ=6√3cm,PR=12cmandQR=6cm then ∠Q is
A45∘B60∘C90∘D120∘In Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
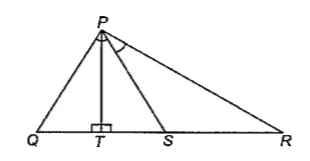 A10B30C60D15
A10B30C60D15
In △PQR,∠Q≻∠R, PS is the bisector of ∠P and PT⊥QR. If ∠SPT=28∘ and ∠R=23∘ , then the measure of ∠Q is:
त्रिभुज PQR में, ∠Q≻∠R, है तथा PS कोण P का समद्विभाजक है और PT⊥QR है । यदि ∠SPT=28∘ और ∠R=23∘ है, तो कोण Q का मान क्या है?
View SolutionIn ΔPQR, if PQ=QR and ∠Q=100°, then ∠R is equal to
View SolutionIn ΔPQR it is given that = PQPR=QSSR. If ∠Q=70∘and∠R=50∘ then ∠QPS = ?
View SolutionIn △PQR, right angled at Q, PQ=105 and QR=208, the value of tanR is:
View SolutionΔPQR is right angled at Q. If ∠R=30∘, then find the value of (cos P -1/3).
View Solution
