In ΔABC , D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABC is divided into four congruent triangles by joining D, E and F.

D is the midpoint of AB
E is the midpoint of BC
So according to midpoint theorem, DE//AC
Similarly, DF//BC and EF//AB
∴ADEF,BDFEandDFCE are
parallelograms
DE is a diagonal of parallelogram,BDFE
∴△BDE≅△FED
similarly△DAF≅△FED
△EFC≅△FED
All four Triangles are congruent
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Given an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
AsquareBrectangleCtrapeziumDrhombus
D, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)View SolutionIn ΔABC,D,E,F are respectively the mid points of the sides AB, BC and AC. Find ratio of the area of ΔDEF and area of ΔABC.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
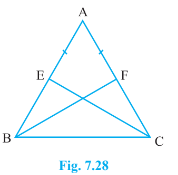 View Solution
View SolutionD, E and F are respectively the mid-points of sides AB. BC and CA of △ABC. Find the ratio of the areas of △DEF and △ABC.
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionIn Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View Solution

