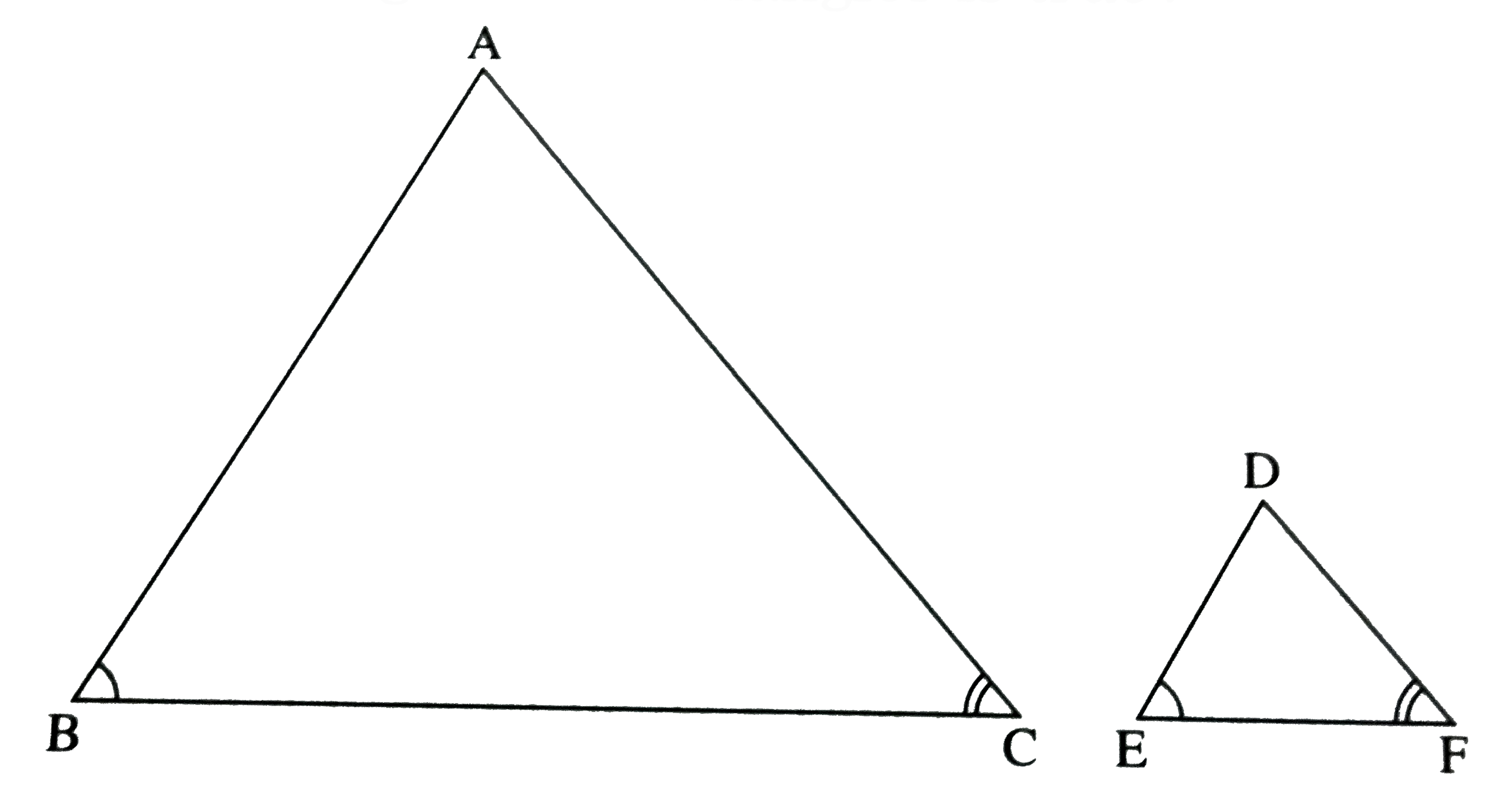
In ΔABCandΔDEF, ∠B=∠E,∠F=∠C and AB = 3 DE, then which of the statements regarding the two triangles is true?
In DeltaABC and DeltaDEF,

A

The triangles are not congruent and not similar.

B

The triangles are similar but not congruent.

C

The triangles are congruent and similar.

D

None of the statements above is true.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

Updated on:21/07/2023
|
Answer

Step by step video & image solution for In DeltaABC and DeltaDEF, " " angleB = angleE, angleF = angleC and AB = 3 DE, then which of the statements regarding the two triangles is true? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023
Class 10MATHSTRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In ΔABCandΔDEF, ∠B=∠E,∠F=∠C and AB=3DE. Then, the two triangles are

    Acongruent but not similar
    Bsimilar but not congruent
    Cneither congruent nor similar
    Dcongruent as well as similar

  • In ΔABCandΔPQR , If AB=AC, ∠C=∠P and ∠B=∠Q, then the two triangles are

    Aisosceles but not congruent
    Bisosceles and congruent
    Ccongruent but not isosceles
    DNeither congruent nor isosceles

  • In ΔABCandΔDEF, it is given that ∠B=∠Eand∠C=∠F, In order that ΔABC≅ΔDEF, we must have

    AAB = DF
    BAC = DE
    CBC = EF
    D∠A=∠D