In □ABCD, seg AD∣∣ seg BC. Diagonal AC and digonal BD intersect each other in point P. Then show that APPD=PCBP.
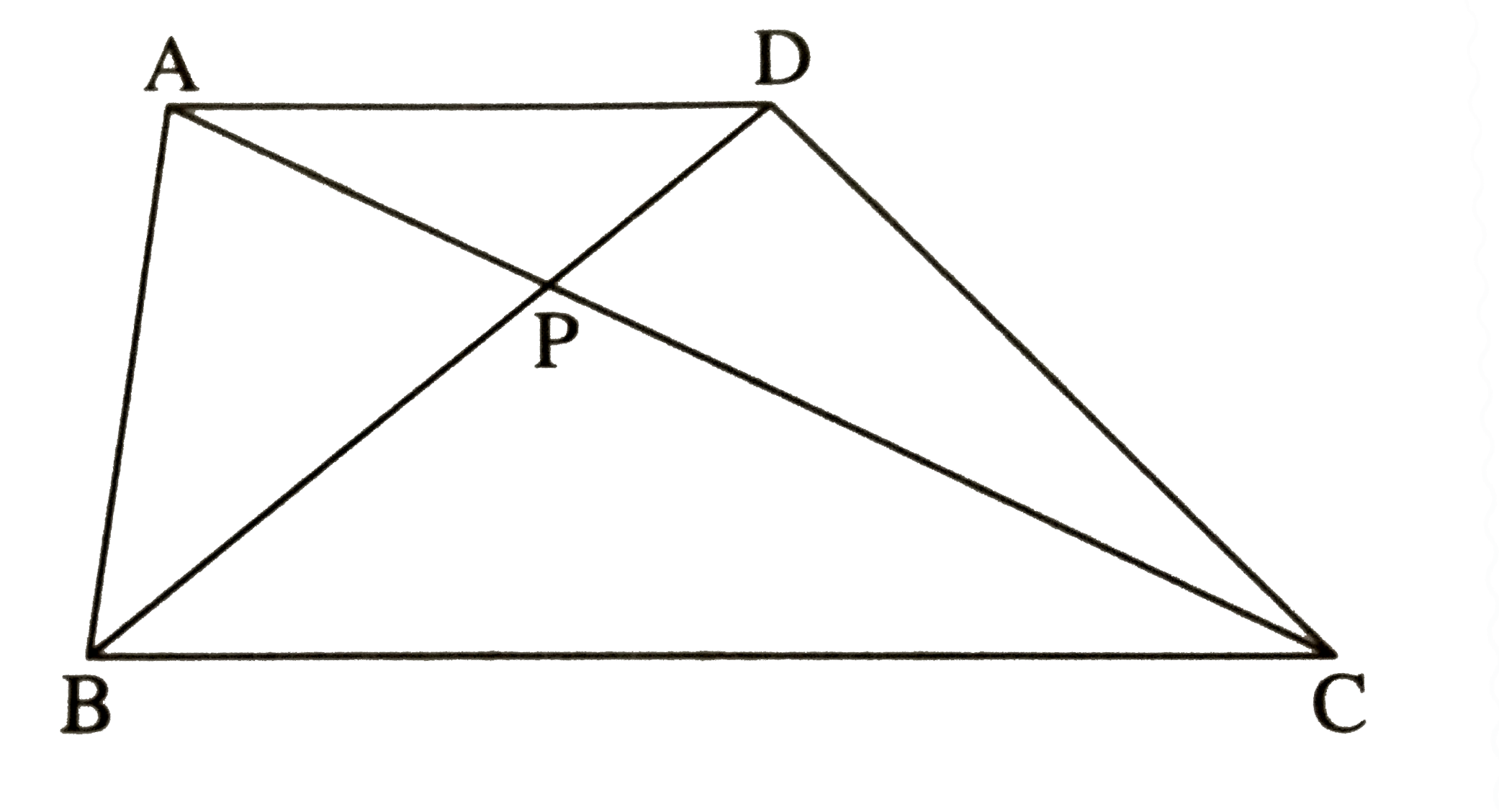
The correct Answer is:∴APPD=PCBP.
Step by step video & image solution for In square ABCD, seg AD|| seg BC. Diagonal AC and digonal BD intersect each other in point P. Then show that (AP)/(PD)=(PC)/(BP). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Activites for Practice4videos
SIMILARITY
- BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Multiple Choice Questions28videos
SIMILARITY
- BOOK - TARGET PUBLICATIONCHAPTER - SIMILARITY EXERCISE - Practice Set 1.47videos
SIMILARITY
- BOOK - TARGET PUBLICATIONCHAPTER - QUESTION FROM STD. IXEXERCISE - Statistics14videos
QUESTION FROM STD. IX
- BOOK - TARGET PUBLICATIONCHAPTER - STATISTICSEXERCISE - Problem Set-621videos
STATISTICS
Similar Questions
Diagonals AC and BD of □ABCD intersect each other at point P. Show that ar(△APB)×ar(△CPD)=ar(△APD)×ar(△BPC)
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that AOBO=CODO.
View SolutionIn □ABCD , side BC∣∣ side AD. Digonals AC and BD intersect each other at P. If AP=13AC then prove DP=12BP.
View SolutionIn the figure, seg AC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
View SolutionIn the figure, set aC and seg BD intersect each other in point P and APCP=BPDP. Prove that ΔABP~ΔCDP.
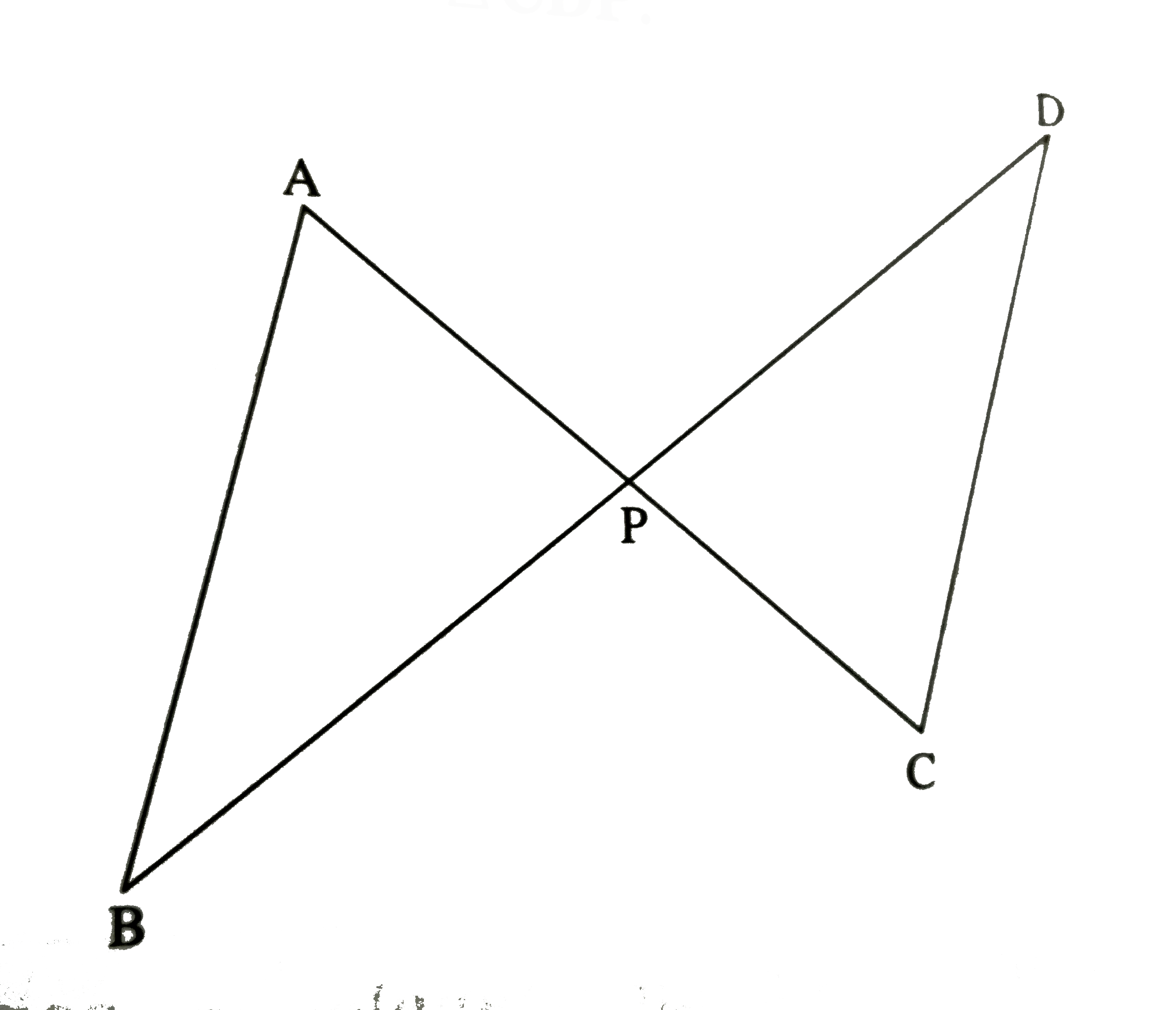 View Solution
View SolutionIn ABCD side BC || side AD. Seg AC and seg BD intersect in point Q. If AQ=1/3 AC then show that DQ=12BQ
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
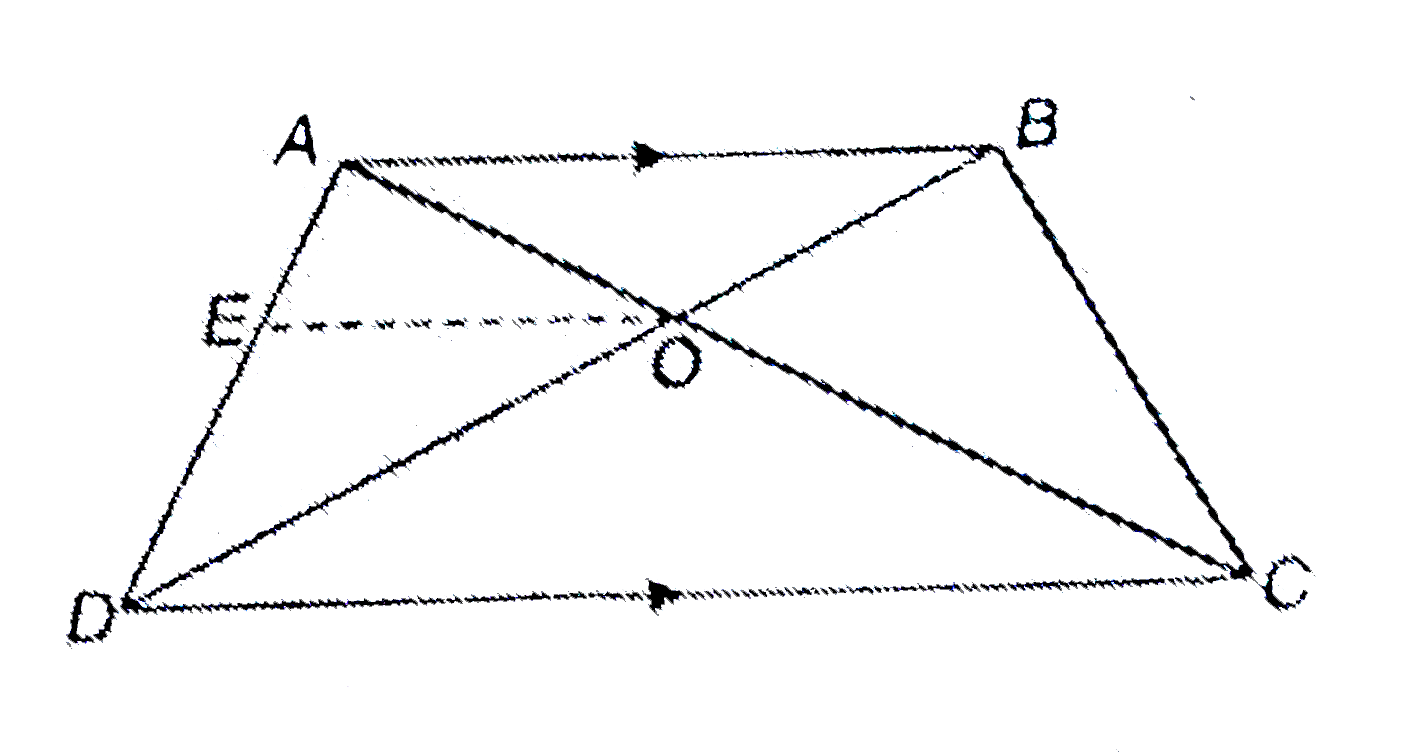 View Solution
View Solutionif ABCD is a trapezium, ACandBD are the diagonals intersecting each other at point Q. then AC:BD=
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionDiagonals ACandBD of a trapezium ABCD with AB∣∣DC intersect each other at O . Prove that ar(AOD)=ar(BOC) .
View Solution

